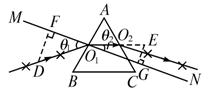
题目内容
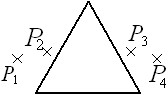 用三棱镜做测定玻璃的折射率的实验,先在白纸上放好三棱镜,在棱镜的一侧插上两枚大头针P1和P2,然后在棱镜的另一侧观察,调整视线使P1的像被P2挡住;接着在眼睛所在的一侧插上两枚大头针P3,P4,使P3挡住P1,P2的像,P4挡住P3和P1,P2的像,在纸上已标明大头针的位置和三棱镜的轮廓
用三棱镜做测定玻璃的折射率的实验,先在白纸上放好三棱镜,在棱镜的一侧插上两枚大头针P1和P2,然后在棱镜的另一侧观察,调整视线使P1的像被P2挡住;接着在眼睛所在的一侧插上两枚大头针P3,P4,使P3挡住P1,P2的像,P4挡住P3和P1,P2的像,在纸上已标明大头针的位置和三棱镜的轮廓(1)在本题的图上画出所需的光路.
(2)为了测出棱镜玻璃的折射率,需要测量的量是
(3)计算折射率的公式n=
(Ⅱ)一个单摆挂在运动电梯中,发现单摆的周期变为电梯静止时周期的2倍,则电梯在这段时间内可能作
分析:(Ⅰ)(1)大头针P1、P2的连线表示入射光线,P3、P4的连线表示出射光线,作出光路图.
(2)(3)研究光线在三棱镜左侧面上折射情况,标出入射角与折射角,根据折射定律得出玻璃砖的折射率表达式.
(Ⅱ)根据单摆的周期公式T=2π
和牛顿第二定律结合分析并求解.
(2)(3)研究光线在三棱镜左侧面上折射情况,标出入射角与折射角,根据折射定律得出玻璃砖的折射率表达式.
(Ⅱ)根据单摆的周期公式T=2π
|
解答:解:(Ⅰ)(1)大头针P1、P2的连线表示入射光线,P3、P4的连线表示出射光线,分别作出入射光线和出射光线,连接入射点和出射点,画出玻璃砖内部光路,画出光路图如图.
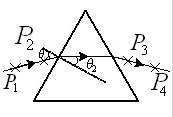 (2)、(3)如图,光线在棱镜左侧面上折射时入射角为i,折射角为r,根据折射定律得到折射率n=
(2)、(3)如图,光线在棱镜左侧面上折射时入射角为i,折射角为r,根据折射定律得到折射率n=
.故需要测量入射角i、折射角r,计算折射率的公式为n=
.
(Ⅱ)电梯静止时,单摆的周期为 T1=2π
摆长不变,而周期变为2倍,说明电梯做加速度不为零的匀变速运动.
在电梯中,单摆的周期为 T2=2π
由题,T2=2T1,则得g′=
摆球静止时,摆线的拉力F=mg′=
mg
取竖直向下方向为正方向,以小球为研究对象,根据牛顿第二定律得
mg-F=ma
解得,a=
g,方向竖直向下,
故 电梯在这段时间内可能匀加速下降或匀减速上升.
故答案为:
(Ⅰ)(1)如右图
(2)入射角i、折射角r
(3)n=
.
(Ⅱ)匀加速下降或匀减速上升,a=
g.
 (2)、(3)如图,光线在棱镜左侧面上折射时入射角为i,折射角为r,根据折射定律得到折射率n=
(2)、(3)如图,光线在棱镜左侧面上折射时入射角为i,折射角为r,根据折射定律得到折射率n=| sini |
| sinr |
| sini |
| sinr |
(Ⅱ)电梯静止时,单摆的周期为 T1=2π
|
摆长不变,而周期变为2倍,说明电梯做加速度不为零的匀变速运动.
在电梯中,单摆的周期为 T2=2π
|
由题,T2=2T1,则得g′=
| g |
| 4 |
摆球静止时,摆线的拉力F=mg′=
| 1 |
| 4 |
取竖直向下方向为正方向,以小球为研究对象,根据牛顿第二定律得
mg-F=ma
解得,a=
| 3 |
| 4 |
故 电梯在这段时间内可能匀加速下降或匀减速上升.
故答案为:
(Ⅰ)(1)如右图
(2)入射角i、折射角r
(3)n=
| sini |
| sinr |
(Ⅱ)匀加速下降或匀减速上升,a=
| 3 |
| 4 |
点评:用插针法测定玻璃砖的实验,基本原理是折射定律,要掌握确定入射光线和出射光线的方法,画光路图时要注意标上箭头.

练习册系列答案
相关题目
 (Ⅰ)有一测量微小时间差的装置,它是由两个摆长略有差别的单摆同轴水平悬挂构成,两个单摆的摆动平面前、后相互平行.
(Ⅰ)有一测量微小时间差的装置,它是由两个摆长略有差别的单摆同轴水平悬挂构成,两个单摆的摆动平面前、后相互平行.