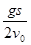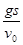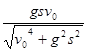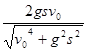题目内容
如图所示,为了把一个大小可忽略的铁块移上台阶,可以采用两种方法:①先用水平力将其沿地面缓慢推到B,再从B缓慢搬到C;②在AC间架设一木板,用与木板平行的力将铁块沿木板缓慢推到C,设铁块和地面、木板间的动摩擦因数相等,两过程中人对铁块做的功分别为W1和W2则( )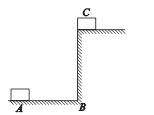
| A.W1>W2 | B.W1<W2 | C.W1=W2 | D.无法比较W1、W2的大小 |
C
解析试题分析:第一种方法人对铁块做的功为W1由动能定理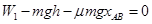 ,第二种方法人对铁块做的功为W2由动能定理
,第二种方法人对铁块做的功为W2由动能定理 ,,而
,,而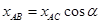 ,解得W1=W2。选项C正确,A、B、D。解决本题的关键第一种方法中沿BC运动无摩擦力做功,运用动能定理求解。
,解得W1=W2。选项C正确,A、B、D。解决本题的关键第一种方法中沿BC运动无摩擦力做功,运用动能定理求解。
考点:动能定理

 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案如图所示,ABCD为匀强电场中相邻的四个等势面(水平),一个电子垂直经过等势面D时,动能为20 eV,飞经等势面C时,电势能为-10 eV,飞至等势面B时速度恰好为0,已知相邻等势面间的距离为5cm,则下列说法正确的是( )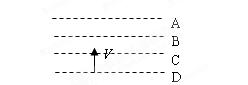
| A.电场强度为200V/m |
| B.电场方向竖直向上 |
| C.等势面A电势为-10V |
| D.电子再次飞经D等势面时,动能为10eV |
一质量为m的实心铅球从离水面一定高度下落并进入足够深的水中,设水对铅球的作用力大小恒为F,则铅球在水中下降h的过程中,下列说法正确的是
| A.铅球的动能减少了Fh |
| B.铅球的机械能减少了(F+mg)h |
| C.铅球的机械能减少了(F-mg)h |
| D.铅球的重力势能减少了mgh |
如图所示,足够长的水平传送带以速度v沿顺时针方向运动,传送带的右端与光滑曲面的底部平滑连接,曲面上的A点距离底部的高度h="0." 45m。一小物体从A点静止滑下,再滑上传送带,经过一段时间又返回曲面。g取10m/s2,则下列说法正确的是( )
| A.若v=1m/s,则小物块能回到A点 |
| B.若v=2m/s,则小物块能回到A点 |
| C.若v=5m/s,则小物块能回到A点 |
| D.无论v等于多少,小物块都不能回到A点 |
带电量均为Q的异种点电荷分别固定在水平方向上的MN两点,其连线中垂线上的O点连接长为L的绝缘轻杆,杆的另一端固定一质量为m,电量为q(q>0)的带电小球,杆可绕O点无摩擦的转动。如图所示,现让小球从O的等高处A点释放,转到最低点B时的速度为v,若C也为O的水平等高点,以无穷远处为电势零点,且q<Q,则
A.A点的电势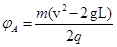 |
B.C点的电势 |
C.A点电势和B点电势的关系是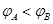 |
D.小球运动到C点的速度大小为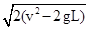 |
起重机将质量为500kg的物体由静止竖直向上吊起2m高,此时物体的速度大小为1m/s,如果g取10m/s2,则
| A.起重机对物体做功250J |
B.起重机对物体做功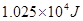 |
| C.物体受到的合力对它做功250J |
D.物体受到的合力对它做功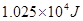 |
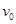 从a点滑上第一块,则物体恰好滑到第三块的末尾d点停下来,物体在运动中地毯保持静止.若让物体从d点以相同的初速度水平向左运动,则物体运动到某一点时的速度大小与该物体向右运动到该位置的速度大小相等,则这一点是( )
从a点滑上第一块,则物体恰好滑到第三块的末尾d点停下来,物体在运动中地毯保持静止.若让物体从d点以相同的初速度水平向左运动,则物体运动到某一点时的速度大小与该物体向右运动到该位置的速度大小相等,则这一点是( )
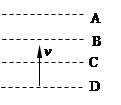
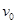 ,射程为
,射程为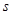 的平抛运动轨迹制成一光滑轨道。一物体由静止开始从轨道顶端滑下,当其到达轨道底部时,物体水平方向速度大小为
的平抛运动轨迹制成一光滑轨道。一物体由静止开始从轨道顶端滑下,当其到达轨道底部时,物体水平方向速度大小为