Question

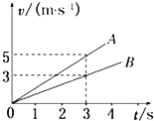
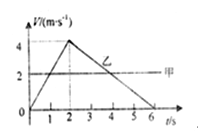
【题目】某次军事演习中，一跳伞队员在t=0时由静止的直升机上跳下，可简化为：先做自由落体运动，在t1速度达到v1时打开降落伞，做减速运动，在t2时刻以速度v2着地，他的速度一时间图像如图所示。（跳伞队员的质量为M，降落伞的质量为m)。据此，下列分析正确的是

A. 在0t时间内，降落伞和跳伞队员的机械能逐渐减小

B. 降落伞打开后降落伞和跳伞队员所受的阻力与速率一定成正比

C. 若第一个跳伞队员跳下后，经过时间t1，第二个跳伞队员跳下，则他们在空中的距离先增大后减小

D. t1t2时间内阻力对降落伞和跳伞队员所做的功为

Answer 1

【答案】C

【解析】试题分析：速度时间图线的斜率表示加速度，根据斜率的变化判断加速度的变化．根据牛顿第二定律判断阻力的变化，根据动能定理求解做功问题．

在时间内运动员做自由落体运动，其间机械能保持不变，后打开降落伞，有阻力做负功，其机械能减小，A错误；由v-t图象知，图线的斜率表示加速度的大小，所以知运动员减速下落过程中加速度越来越小，所受阻力越来越小，但由图线无法判断阻力大小与速度成正比，B错误；若第一个伞兵在空中打开降落伞时第二个伞兵立即跳下，由于第一个伞兵的速度先大于第二个伞兵的速度，然后又小于第二个伞兵的速度，所以空中的距离先增大后减小，C正确；根据动能定理，合外力对跳伞队员和降落伞做的功等于其动能的变化，因为在的时间内，重力对他们做功，故其阻力做功等于的功为，故D错误．