题目内容
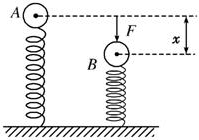
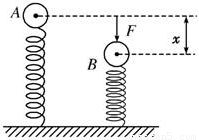
如图所示，轻弹簧的劲度系数为k，小球的质量为m，平衡时小球在A位置．今用力F将小球向下压缩x至B位置．则此时弹簧的弹力大小为（ ）分析：胡克定律：F=kx，F为弹力，k是劲度系数，x为形变量，找出形变量代入胡克定律求解．
解答：解：当弹簧处于平衡位置A时：设弹簧的形变量为x1，由胡克定律得：
mg=kx1
解得：x1=
小球向下压缩x至B位置时，小球的形变量x2=
+x
由胡克定律得：
F=kx2
即：F=k×（
+x）=mg+kx
故选：C
mg=kx1
解得：x1=
| mg |
| k |
小球向下压缩x至B位置时，小球的形变量x2=
| mg |
| k |
由胡克定律得：
F=kx2
即：F=k×（
| mg |
| k |
故选：C
点评：本题是胡克定律的应用，关键点在于找形变量x，找出形变量代入胡克定律即可．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，轻弹簧的劲度系数为k，小球的质量为m，平衡时小球在A位置．今用力F将小球向下压缩x至新的平衡位置B，则此时弹簧的弹力大小为（ ）
