题目内容
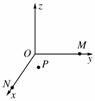
空间有一匀强电场,在电场中建立直角坐标系O-xyz,M、N、P为电场中的三点,点M的坐标(0,a,0),点N的坐标(a,0,0),点P的坐标(a,
,
).已知电场方向平行于直线MN,点M的电势为0,点N的电势为1V,把一个电子从点P移到N电场力做功为( )
| a |
| 2 |
| a |
| 2 |
分析:将电场强度沿坐标轴方向正交分解,先求出各个电场力的分量做的功,然后运用合力的功等于各个分力的功的代数和求合力的功.
解答:解:根据题意已知电场方向平行于直线MN,点M的电势为0,点N的电势为1V,故
UNM=E?
a=1V ①
将电场强度沿着-x方向和+y方向正交分解,设合场强为E,则-x和+y方向的分量分别为:
Ex=
E,Ey=
E ②
电场力做功与路径无关,只与初末位置有关,设P在x0y平面上的投影为P′点,将一电子从P点经过P′移到N点,电场力沿z方向和x方向分量做功均为0,电场力y方向分量做功为qEy?
,故电场力做的总功为W=qEy?
=qE
a ③;
由①②③式求得电场力做的总功为W=
eV
故选C.
UNM=E?
| 2 |
将电场强度沿着-x方向和+y方向正交分解,设合场强为E,则-x和+y方向的分量分别为:
Ex=
| ||
| 2 |
| ||
| 2 |
电场力做功与路径无关,只与初末位置有关,设P在x0y平面上的投影为P′点,将一电子从P点经过P′移到N点,电场力沿z方向和x方向分量做功均为0,电场力y方向分量做功为qEy?
| a |
| 2 |
| a |
| 2 |
| ||
| 4 |
由①②③式求得电场力做的总功为W=
| 1 |
| 4 |
故选C.
点评:本题关键运用正交分解法,将电场力沿着坐标轴方向正交分解,然后先计算各个分电场力做的功,再计算电场力的总功.

练习册系列答案
相关题目
 空间有一匀强电场,在电场中建立如图所示的直角坐标系O-xyz,M、N、P为电场中的三个点,M点的坐标(0,a,0),N点的坐标为(a,0,0),P点(图中未画出)的坐标为 (
空间有一匀强电场,在电场中建立如图所示的直角坐标系O-xyz,M、N、P为电场中的三个点,M点的坐标(0,a,0),N点的坐标为(a,0,0),P点(图中未画出)的坐标为 (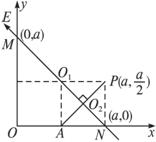

 V
V
 V
V