题目内容
10.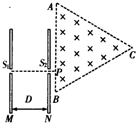 如图所示,M、N为中心开有小孔的平行板电容器的两极板,相距为D,其右侧有一边长为2a的正三角形区域,区域内有垂直纸面向里的匀强磁场,在极板M、N之间加上电压U后,M板电势高于N板电势.现有一带正电的粒子,质量为m、电荷量为q,其重力和初速度均忽略不计,粒子从极板M的中央小孔S1处射入电容器,穿过小孔S2后从距三角形A点$\sqrt{3}$a的P处垂直AB方向进入磁场,试求:
如图所示,M、N为中心开有小孔的平行板电容器的两极板,相距为D,其右侧有一边长为2a的正三角形区域,区域内有垂直纸面向里的匀强磁场,在极板M、N之间加上电压U后,M板电势高于N板电势.现有一带正电的粒子,质量为m、电荷量为q,其重力和初速度均忽略不计,粒子从极板M的中央小孔S1处射入电容器,穿过小孔S2后从距三角形A点$\sqrt{3}$a的P处垂直AB方向进入磁场,试求:(1)粒子到达小孔S2时的速度;
(2)若粒子从P点进入磁场后经时间t从AP间离开磁场,求粒子的运动半径和磁感应强度的大小;
(3)若粒子能从AC间离开磁场,磁感应强度应满足什么条件?
分析 (1)粒子在加速电场中,电场力做功,由动能定理求出速度v,根据运动学公式求出所以时间.
(2)粒子从进入磁场到从AD间离开,根据半径公式,周期公式结合几何关系即可求解;
(3)粒子从进入磁场到从AC间离开,画出运动轨迹,找出临界状态,根据半径公式结合几何关系即可求解;
解答 解:(1)带电粒子在电场中运动时,由动能定理得,qU=$\frac{1}{2}m{v}^{2}$,
解得粒子进入磁场时的速度大小为v=$\sqrt{\frac{2qU}{m}}$.
(2)粒子的轨迹图如图所示,粒子从进入磁场到AP间离开,由牛顿第二定律可得,$qvB=m\frac{{v}^{2}}{R}$,
粒子在磁场中运动的时间为t=$\frac{πR}{v}$,
由以上两式可得轨道半径R=$\frac{\sqrt{2qUm}}{πm}t$,
磁感应强度B=$\frac{πm}{qt}$.
(3)粒子从进入磁场到从AC间离开,若粒子恰能到达BC边界,如图所示,设此时的磁感应强度为B1,根据几何关系有此时粒子的轨道半径为${R}_{1}=2asin60°=\sqrt{3}a$,
由牛顿第二定律可得,$q{vB}_{1}=m\frac{{v}^{2}}{{R}_{1}}$,
由以上两式可得${B}_{1}=\frac{\sqrt{6qUm}}{3qa}$,
粒子从进入磁场到从AC间离开,若粒子恰能到达AC边界,如图所示,设此时的磁感应强度为B2,
由牛顿第二定律可得,$qv{B}_{2}=m\frac{{v}^{2}}{{R}_{2}}$,
由以上两式解得${B}_{2}=\frac{(2+\sqrt{3})\sqrt{2qUm}}{3qa}$.
综上所述要使粒子能从AC间离开磁场,磁感应强度应满足:$\frac{\sqrt{6qUm}}{3qa}≤B≤\frac{(2+\sqrt{3})\sqrt{2qUm}}{3qa}$.
答:(1)粒子到达小孔S2时的速度为$\sqrt{\frac{2qU}{m}}$.
(2)粒子的运动半径为$\frac{\sqrt{2qUm}}{πm}t$,磁感应强度的大小为$\frac{πm}{qt}$.
(3)磁感应强度应满足$\frac{\sqrt{6qUm}}{3qa}≤B≤\frac{(2+\sqrt{3})\sqrt{2qUm}}{3qa}$.
点评 本题是带电粒子在组合场中运动的问题,粒子在磁场中做匀速圆周运动,要求同学们能画出粒子运动的轨迹,能根据半径公式,周期公式结合几何关系求解,难度较大.

 小学课时特训系列答案
小学课时特训系列答案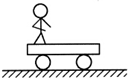 如图所示,光滑的水平地面上有一辆平板车,车上有一个人.原来车和人都静止.当人从左向右行走的过程中( )
如图所示,光滑的水平地面上有一辆平板车,车上有一个人.原来车和人都静止.当人从左向右行走的过程中( )| A. | 人和车组成的系统水平方向动量不守恒 | |
| B. | 人和车组成的系统机械能守恒 | |
| C. | 人和车的速度方向相同 | |
| D. | 人停止行走时,人和车的速度一定均为零 |
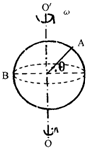 花式篮球是年青人酷爱的一项运动,图示为某同学在单指转篮球,篮球绕中心线OO′匀速转动,A、B为篮球表面不同位置的两点,则( )
花式篮球是年青人酷爱的一项运动,图示为某同学在单指转篮球,篮球绕中心线OO′匀速转动,A、B为篮球表面不同位置的两点,则( )| A. | B点的角速度大于A点角速度 | B. | A、B两点线速度大小相等 | ||
| C. | A、B两点的周期相等 | D. | A、B两点向心加速度大小相等 |
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
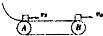 如图所示,水平传送带A、B两端相距x=3.5m,物体与传送带间的动摩擦因数μ=0.1,物体滑上传送带A端的瞬时速度vA=4m/s,到达B端的瞬时速度设为vB,下列说法中正确的是( )
如图所示,水平传送带A、B两端相距x=3.5m,物体与传送带间的动摩擦因数μ=0.1,物体滑上传送带A端的瞬时速度vA=4m/s,到达B端的瞬时速度设为vB,下列说法中正确的是( )| A. | 若传送带逆时针匀速转动,vB一定等于3m/s | |
| B. | 若传送带逆时针匀速转动越快,vB越小 | |
| C. | 若传送带顺时针匀速转动,vB有可能等于3m/s | |
| D. | 若传送带顺时针匀速转动,物体刚开始滑上传送带A端时一定做匀加速运动 |
| A. | 光的双缝干涉实验中,若仅将入射光由红光改为紫光,则相邻亮条纹间距一定变大 | |
| B. | 在受迫振动中,驱动力的频率不一定等于物体的固有频率 | |
| C. | 宇航员驾驶宇宙飞船以接近光速经过地球时,地球上的人观察到飞船上的时钟变快 | |
| D. | 光能够发生偏振现象说明光是横波 | |
| E. | 光导纤维传播光信号利用了光的全反射原理 |
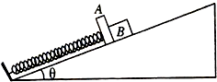 如图所示,在倾角为θ的斜面上,轻质弹簧一端与斜面底端固定,另一端与质量为M的物体A连接,一个质量为m的物体B靠在A上,A、B与斜面的动摩擦因数均为μ.开始时用手按住物体B使弹簧处于压缩状态.现放手,使A、B一起沿斜面向上运动距离L时,A、B达到最大速度v,重力加速度为g.下列说法正确的是( )
如图所示,在倾角为θ的斜面上,轻质弹簧一端与斜面底端固定,另一端与质量为M的物体A连接,一个质量为m的物体B靠在A上,A、B与斜面的动摩擦因数均为μ.开始时用手按住物体B使弹簧处于压缩状态.现放手,使A、B一起沿斜面向上运动距离L时,A、B达到最大速度v,重力加速度为g.下列说法正确的是( )| A. | A、B达到最大速度v时,弹簧处于自然长度 | |
| B. | 若运动过程中A、B能够分离,则A、B恰好分离时,二者加速度大小均为g(sinθ+μcosθ ) | |
| C. | 从释放到A、B达到最大速度v的过程中,B受到的合力对它做的功等于$\frac{1}{2}$mv2 | |
| D. | 从释放到A、B达到最大速度v的过程中,弹簧对A所做的功等于$\frac{1}{2}$Mv2+MgLsinθ+μMgLcosθ |
| A. | $\frac{p}{q}$ | B. | $\frac{q}{p}$ | C. | $\frac{p+q}{p}$ | D. | $\frac{p+q}{q}$ |
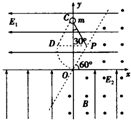 如图所示,在xOy竖直平面内,长L的绝缘轻绳一端固定在第一象限的P点,另一端栓有一质量为m、带电荷量为+q的小球,OP距离也为L且与x轴的夹角为60°.在x轴上方有水平向左的匀强电场,场强大小为$\frac{\sqrt{3}mg}{3q}$,在x轴下方有竖直向上的匀强电场,场强大小为$\frac{mg}{q}$,过O和P两点的虚线右侧存在方向垂直xOy平面向外、磁感应强度为B的匀强磁场.小球置于y轴上的C点时,绳恰好伸直且与y轴夹角为30°,小球由静止释放后将沿CD方向做直线运动,到达D点时绳恰好绷紧,小球沿绳方向的分速度立即变为零,并以垂直于绳方向的分速度摆下,到达O点时将绳断开.不计空气阻力.求:
如图所示,在xOy竖直平面内,长L的绝缘轻绳一端固定在第一象限的P点,另一端栓有一质量为m、带电荷量为+q的小球,OP距离也为L且与x轴的夹角为60°.在x轴上方有水平向左的匀强电场,场强大小为$\frac{\sqrt{3}mg}{3q}$,在x轴下方有竖直向上的匀强电场,场强大小为$\frac{mg}{q}$,过O和P两点的虚线右侧存在方向垂直xOy平面向外、磁感应强度为B的匀强磁场.小球置于y轴上的C点时,绳恰好伸直且与y轴夹角为30°,小球由静止释放后将沿CD方向做直线运动,到达D点时绳恰好绷紧,小球沿绳方向的分速度立即变为零,并以垂直于绳方向的分速度摆下,到达O点时将绳断开.不计空气阻力.求: