题目内容
假设探月宇航员站在月球表面一斜坡上的M点，并沿水平方向以初速度v0抛出一个质量为m的小球，测得小球经时间t落到斜坡上另一点N，斜面的倾角为α，已知月球半径为R，月球的质量分布均匀，万有引力常量为G，求：
（1）月球表面的重力加速度g′；
（2）人造卫星绕月球做匀速圆周运动的最大速度．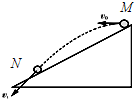
（1）月球表面的重力加速度g′；
（2）人造卫星绕月球做匀速圆周运动的最大速度．
（1）小球做平抛运动，水平位移x=υ0t，竖直位移y=
g′t2，
由位移关系得：tanα=
=
，g′=
；
（2）人造卫星绕月球做圆周运动的向心力由万有引力提供，
=m
①，
月球表面物体所受重力等于万有引力，
=mg′②，
由①②得υ=
；
答：（1）月球表面的重力加速度g′=
；
（2）人造卫星绕月球做匀速圆周运动的最大速度是υ=
．
| 1 |
| 2 |
由位移关系得：tanα=
| y |
| x |
| ||
| v0t |
| 2v0tanα |
| t |
（2）人造卫星绕月球做圆周运动的向心力由万有引力提供，
| GMm |
| R2 |
| v2 |
| R |
月球表面物体所受重力等于万有引力，
| GMm′ |
| R2 |
由①②得υ=
|
答：（1）月球表面的重力加速度g′=
| 2v0tanα |
| t |
（2）人造卫星绕月球做匀速圆周运动的最大速度是υ=
|
练习册系列答案
阅读快车系列答案
相关题目
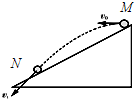（2011?湖北模拟）假设探月宇航员站在月球表面一斜坡上的M点，并沿水平方向以初速度v0抛出一个质量为m的小球，测得小球经时间t落到斜坡上另一点N，斜面的倾角为α，已知月球半径为R，月球的质量分布均匀，万有引力常量为G，求：
，已知月球半径为R，月球的质量分布均匀，万有引力常量为G，求：
；
，已知月球半径为R，月球的质量分布均匀，万有引力常量为G，求：
；
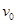竖直上抛一小球，经过时间t小球落回原处，已知月球半径为R，月球的质量分布均匀，万有引力常量为G，求：
；
；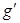