题目内容
(12分)在倾角为θ的光滑斜面上端系有一劲度系数为k的弹簧,弹簧轴线与斜面平行,弹簧下端连一个质量为m的小球,球被一垂直斜面的挡板A挡住,此时弹簧没有形变,若A以加速度a(a<gsinθ)沿斜面向下匀加速运动,求:
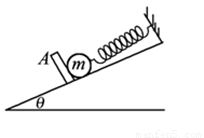
(1)从挡板开始运动到球板分离所经历的时间t.
(2)从挡板开始运动到小球速度最大时,球的位移x.
【答案】
(1)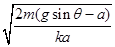 (2)mgsinθ/k.
(2)mgsinθ/k.
【解析】
试题分析:(1)设球与挡板分离时位移为s,经历的时间为t,从开始运动到分离过程中,m受到竖直向下的重力,垂直斜面向上的支持力FN,沿斜面向上的挡板支持力FN1和弹簧弹力f,根据牛顿第二定律可得方程:
mgsinθ-f-FN1=ma,又因f=kx
随着x的增大,f增大,FN1减小,保持a不变,当m与挡板分离时,x增大到等于s,FN1减小到0,则有:
x=at2/2,mgsinθ-kx=ma
联立解得t=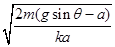
(2)分离后继续做加速度减小的加速运动,v最大时,m受合力为零,即kxm=mgsinθ
位移是xm=mgsinθ/k.
考点:本题考查牛顿第二定律、运动学关系和胡克定律。

练习册系列答案
相关题目
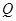 的正点电荷。O为AB连线的中点,a、b是AB连线上两点,其中Aa=Bb=
的正点电荷。O为AB连线的中点,a、b是AB连线上两点,其中Aa=Bb=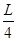 。一质量为m、电荷量为+q的小滑块(可视为质点)以初动能
。一质量为m、电荷量为+q的小滑块(可视为质点)以初动能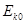 从a点出发,沿AB直线向b点运动,其中小滑块第一次经过O点时的动能为
从a点出发,沿AB直线向b点运动,其中小滑块第一次经过O点时的动能为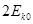 ,第一次到达b点时的动能恰好为零,已知静电力常量为
,第一次到达b点时的动能恰好为零,已知静电力常量为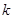 。求:
。求: