题目内容
(12分)光滑平行的金属导轨MN和PQ的间距L＝1.0 m，它们与水平面之间的夹角α＝30°，匀强磁场的磁感应强度B＝2.0 T，方向垂直于导轨平面向上，M、P间连接有阻值R＝2.0 Ω 的电阻，其他电阻不计，质量m＝2.0 kg的金属杆ab垂直于导轨放置，如图甲所示．用恒力F沿导轨平面向上拉金属杆ab，使其由静止开始运动，其v－t图象如图乙所示．取g＝10 m/s2，设导轨足够长．
(1)求恒力F的大小．
(2)金属杆的速度为2.0 m/s时，加速度为多大？
(3)根据v－t图象估算在前0.8 s内电阻上产生的热量．
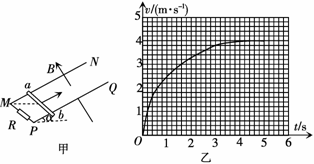
【解析】(1)由图乙知，杆运动的最大速度vm＝4 m/s (2分)
此时有：F＝mgsin α＋F安
＝mgsin α＋
(1分)
代入数据得：F＝18 N． (1分)
(2)对杆进行受力分析，如图丙所示，由牛顿第二定律可得：
F－F安－mgsin α＝ma (1分)
a＝
代入数据得：a＝2.0 m/s2． (1分)
(3)由图乙可知，0.8 s末金属杆的速度v1＝2.2 m/s (1分)
前 0.8 s 内图线与t轴所包围的小方格的个数约为27，面积为27×0.2×0.2＝1.08，即前0.8 s内金属杆的位移为：
s＝1.08 m (2分)
由能的转化与守恒定律得：
Q＝Fs－mgssin α－
mv12 (2分)
代入数据得：Q＝3.80 J． (1分)
[答案] (1)18 N (2)2.0 m/s2 (3)3.80 J
丙
练习册系列答案
轻松暑假总复习系列答案
相关题目
