Question

(12分)如图所示，倾角θ=30°、宽度L="1" m的足够长的U形平行光滑金属导轨，固定在磁感应强度B="1" T、范围充分大的匀强磁场中，磁场方向与导轨平面垂直。用平行于导轨、功率恒为6 W的牵引力F牵引一根质量为m="0.2" kg、电阻R="1" Ω的放在导轨上的金属棒ab，由静止开始沿导轨向上移动(ab始终与导轨接触良好且垂直)。当ab棒移动2.8 m时，获得稳定速度，在此过程中，克服安培力做功为5.8 J(不计导轨电阻及一切摩擦，g取10 m/s²)，求：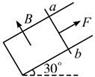

(1)ab棒的稳定速度。
(2)ab棒从静止开始达到稳定速度所需时间。

Answer 1

(1)v="2" m/s  (2)t="1.5" s

解析试题分析：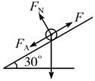  

当棒速稳定时棒受力平衡。设此时棒速为v。则有：
(1)P=Fv                          ①
F=mgsinθ+F_安              ②
F_安=BIL                        ③
I=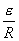    ④     ε=BLv  ⑤    由①—⑤得到：v²+v-6=0  v="2" m/s(负值舍去)
(2)由动能定理得：W_F-W_安-mgh=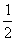mv²           ⑥            
W^F=Pt             ⑦
h="Ssin30°=2.8sin30°" m="1.4" m              ⑧
联立得到：t=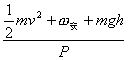代入数据得t="1.5" s
考点：考查了导体切割磁感线运动
点评：做此类型的题目需要根据受力分析，结合力的平衡条件，动能定理等解题