题目内容
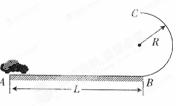
 某兴趣小组举行遥控赛车比赛,比赛路径如图所示.可视为质点的赛车从起点A出发,沿水平直线轨道运动L=10m后,由B点进入半径R=0.4m的光滑竖直半圆轨道,并通过轨道的最高点C做平抛运动,落地后才算完成比赛.B是半圆轨道的最低点,水平直线轨道和半圆轨道相切于B点.已知赛车质量m=0.5Kg,通电后电动机以额定功率P=3W工作,赛车在水平轨道上受到的阻力恒为f=0.4N,之后在运动中受到的轨道阻力均可不计,g取10m/s2.试求:
某兴趣小组举行遥控赛车比赛,比赛路径如图所示.可视为质点的赛车从起点A出发,沿水平直线轨道运动L=10m后,由B点进入半径R=0.4m的光滑竖直半圆轨道,并通过轨道的最高点C做平抛运动,落地后才算完成比赛.B是半圆轨道的最低点,水平直线轨道和半圆轨道相切于B点.已知赛车质量m=0.5Kg,通电后电动机以额定功率P=3W工作,赛车在水平轨道上受到的阻力恒为f=0.4N,之后在运动中受到的轨道阻力均可不计,g取10m/s2.试求:(1)赛车能通过C点完成比赛,其落地点离B点的最小距离
(2)要使赛车完成比赛,电动机工作的最短时间.
(3)若赛车过B点速度vB=8.0m/s,R为多少时赛车能完成比赛,且落地点离B点的最大距离.
分析:(1)小车做圆周运动,在最高点重力提供向心力时速度最小,由牛顿第二定律可以求出最小速度,离开C后做平抛运动,由平抛运动知识可以求出小车的水平位移.
(2)从A到C应用动能定理可以求出电动机的工作时间.
(3)由B到C由机械能守恒定律或动能定理求出到C的速度,离开C后小车做平抛运动,由平抛运动知识求出小车水平位移的表达式,然后求出最大水平位移.
(2)从A到C应用动能定理可以求出电动机的工作时间.
(3)由B到C由机械能守恒定律或动能定理求出到C的速度,离开C后小车做平抛运动,由平抛运动知识求出小车水平位移的表达式,然后求出最大水平位移.
解答:解:(1)赛车以最小速度通过最高点C,其落地点离B点的距离最小,在最高点C由牛顿第二定律得:mg=m
,解得:vC=
=2m/s,离开C后小车做平抛运动,
在水平方向:x=vCt,在竖直方向:2R=
gt2,解得:x=0.8m;
(2)设电动机工作的最短时间为t,赛车从A到C过程,由动能定理得:
Pt-fL-2mgR=
m
-0
解得:t=3s;
(3)设轨道半径为R,B到C过程赛车机械能守恒得:
m
=mg2R+
m
vc=
,
赛车离开C点后做平抛运动,设水平位移为x,
在水平方向:x=vCt,在竖直方向:2R=
gt2,
解得:x=
=
,
当
-4R=4R时,即R=0.80m时,最大水平位移为xm=3.2m;
答:(1)赛车能通过C点完成比赛,其落地点离B点的最小距离为0.8m;
(2)要使赛车完成比赛,电动机工作的最短时间为3s.
(3)若赛车过B点速度vB=8.0m/s,R为0.8m时赛车能完成比赛,且落地点离B点的最大距离为3.2m.
| ||
| R |
| gR |
在水平方向:x=vCt,在竖直方向:2R=
| 1 |
| 2 |
(2)设电动机工作的最短时间为t,赛车从A到C过程,由动能定理得:
Pt-fL-2mgR=
| 1 |
| 2 |
| v | 2 c |
解得:t=3s;
(3)设轨道半径为R,B到C过程赛车机械能守恒得:
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 c |
vc=
|
赛车离开C点后做平抛运动,设水平位移为x,
在水平方向:x=vCt,在竖直方向:2R=
| 1 |
| 2 |
解得:x=
|
|
(
|
当
| ||
| g |
答:(1)赛车能通过C点完成比赛,其落地点离B点的最小距离为0.8m;
(2)要使赛车完成比赛,电动机工作的最短时间为3s.
(3)若赛车过B点速度vB=8.0m/s,R为0.8m时赛车能完成比赛,且落地点离B点的最大距离为3.2m.
点评:分析清楚小车的运动过程,应用牛顿第二定律、动能定理、平抛运动知识即可正确解题.

练习册系列答案
相关题目