Question

图中MN表示真空室中垂直于纸面的平板，它的一侧有匀强磁场，磁场方向垂直于纸面向里，磁感应强度大小为B。一带正电粒子从平板上狭缝O处以与平板成θ的初速度v射入磁场区域如图，最后到达平板上的P点。已知B、v以及P到O的距离l，不计重力，求此粒子的电荷量q与质量m之比。

Answer 1

 

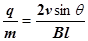
试题分析：带电粒子从O点垂直射入磁场，在洛伦兹力作用下做匀速圆周运动．又从P点射出磁场，则PO连线就是运动圆弧的直径，由长度、运动速度及磁场可确定粒子的比荷．
解：（1）由左手定则可知：粒子带正电

（2）粒子在磁场中做匀速圆周运动，设其半径为R ，
由几何关系可知：
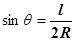
由洛伦兹力公式和牛顿第二定律，有
qvB=m
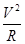
由此得  
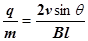
点评：将带电粒子的入射点与出射点连线，即为圆弧对应的弦．当圆心落在弦上，则弦就是直径．