题目内容
2. 如图,拉格朗日点L1位于地球和月球连线上,处在该点的物体在地球和月球引力的共同作用下,可与月球一起以相同的周期绕地球运动.据此,科学家设想在拉格朗日点L1建立空间站,使其与月球同周期绕地球运动,以a1、a2分别表示该空间站和月球向心加速度的大小,a3表示地球同步卫星向心加速度的大小.以下判断正确的是( )
如图,拉格朗日点L1位于地球和月球连线上,处在该点的物体在地球和月球引力的共同作用下,可与月球一起以相同的周期绕地球运动.据此,科学家设想在拉格朗日点L1建立空间站,使其与月球同周期绕地球运动,以a1、a2分别表示该空间站和月球向心加速度的大小,a3表示地球同步卫星向心加速度的大小.以下判断正确的是( )| A. | a2>a3>a1 | B. | a2>a1>a3 | C. | a3>a1>a2 | D. | a3>a2>a1 |
分析 由题意知,空间站在L1点能与月球同步绕地球运动,其绕地球运行的周期、角速度等于月球绕地球运行的周期、角速度,
由an=$\frac{{4π}^{2}}{{T}^{2}}$r,分析向心加速度a1、a2的大小关系.根据a=$\frac{GM}{{r}^{2}}$分析a3与a1、a2的关系.
解答 解:在拉格朗日点L1建立空间站,使其与月球同周期绕地球运动,
根据向心加速度an=$\frac{{4π}^{2}}{{T}^{2}}$r,
由于拉格朗日点L1的轨道半径小于月球轨道半径,所以a2>a1,
同步卫星离地高度约为36000公里,故同步卫星离地距离小于拉格朗日点L1的轨道半径,
根据a=$\frac{GM}{{r}^{2}}$得a3>a2>a1,
故选:D.
点评 本题比较简单,对此类题目要注意掌握万有引力充当向心力和圆周运动向心加速度公式的联合应用.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
12.把两个大小相同的实心铝球和实心铁球放在同一水平面上,它们的重力势能分别为E1和E2.若把它们移至另一个较低的水平面上时,它们的重力势能减少量分别为△E1和△E2则必有( )
| A. | E1<E2 | B. | E1>E2 | C. | △E1<△E2 | D. | △E1<△E2 |
7.墨滴入水,扩而散之,徐徐混匀.关于该现象的分析正确的是( )
| A. | 混合均匀主要是由于碳粒受重力作用 | |
| B. | 混合均匀的过程中,水分子和碳粒都做无规则运动 | |
| C. | 使用碳粒更小的墨汁,混合均匀的过程进行得更迅速 | |
| D. | 墨汁的扩散运动是由于碳粒和水分子发生化学反应引起的 |
14.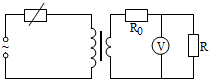 如图,一理想变压器原、副线圈匝数之比为4:1,原线圈与一可变电阻串联后,接入一正弦交流电源;副线圈电路中固定电阻的阻值为R0,负载电阻的阻值R=11R0,
如图,一理想变压器原、副线圈匝数之比为4:1,原线圈与一可变电阻串联后,接入一正弦交流电源;副线圈电路中固定电阻的阻值为R0,负载电阻的阻值R=11R0, 是理想电压表.现将负载电阻的阻值减小为R=5R0,保持变压器输入电流不变,此时电压表的读数为5.0V,则( )
是理想电压表.现将负载电阻的阻值减小为R=5R0,保持变压器输入电流不变,此时电压表的读数为5.0V,则( )
 如图,一理想变压器原、副线圈匝数之比为4:1,原线圈与一可变电阻串联后,接入一正弦交流电源;副线圈电路中固定电阻的阻值为R0,负载电阻的阻值R=11R0,
如图,一理想变压器原、副线圈匝数之比为4:1,原线圈与一可变电阻串联后,接入一正弦交流电源;副线圈电路中固定电阻的阻值为R0,负载电阻的阻值R=11R0, 是理想电压表.现将负载电阻的阻值减小为R=5R0,保持变压器输入电流不变,此时电压表的读数为5.0V,则( )
是理想电压表.现将负载电阻的阻值减小为R=5R0,保持变压器输入电流不变,此时电压表的读数为5.0V,则( )| A. | 此时原线圈两端电压的最大值约为34V | |
| B. | 此时原线圈两端电压的最大值约为24V | |
| C. | 原线圈两端原来的电压有效值约为68V | |
| D. | 原线圈两端原来的电压有效值约为48V |

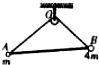 如图所示,两个质量分别为m,4m的质点A、B之间用轻杆连结,并通过长为L的轻绳挂在光滑的定滑轮上,求系统平衡时OA,OB段绳长各为多少.
如图所示,两个质量分别为m,4m的质点A、B之间用轻杆连结,并通过长为L的轻绳挂在光滑的定滑轮上,求系统平衡时OA,OB段绳长各为多少. 如图所示,质量为m的木块A以水平速度v0冲上了质量为M长为L,置于光滑水平面上的木板B,并正好不从B木板上掉下.(当A刚滑到B右端是恰好达到共同的速度),A,B间的动摩擦因数为μ,求:
如图所示,质量为m的木块A以水平速度v0冲上了质量为M长为L,置于光滑水平面上的木板B,并正好不从B木板上掉下.(当A刚滑到B右端是恰好达到共同的速度),A,B间的动摩擦因数为μ,求: 如图所示,质量为M=5kg的圆形汽缸内部底面横截面积为s=10cm2,内部高为l=0.8m,放置在水平地面上(与地面间有少量空隙),汽缸中用质量为m=2kg的光滑活塞封闭了一定质量的理想气体,开始时气柱长度为l1=0.4m,现用力缓慢拉动活塞,整个过程气体温度保持不变,已知大气压强为P0=1×105Pa,g取10m/s2.
如图所示,质量为M=5kg的圆形汽缸内部底面横截面积为s=10cm2,内部高为l=0.8m,放置在水平地面上(与地面间有少量空隙),汽缸中用质量为m=2kg的光滑活塞封闭了一定质量的理想气体,开始时气柱长度为l1=0.4m,现用力缓慢拉动活塞,整个过程气体温度保持不变,已知大气压强为P0=1×105Pa,g取10m/s2.