题目内容
【题目】某空间存在一竖直向下的匀强电场和圆形区域的匀强磁场，磁感应强度为B，方向垂直纸面向里，如图所示．一质量为m，带电量为+q的粒子，从P点以水平速度v0射入电场中，然后从M点射入磁场，从N点射出磁场．已知，带电粒子从M点射入磁场时，速度与竖直方向成30°角，弧MN是圆周长的 
，粒子重力不计．求：
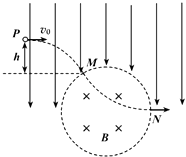
（1）电场强度E的大小．
（2）圆形区域的半径R．
（3）带电粒子从P点到N点，所经历的时间t．
【答案】
（1）解：在电场中，粒子经过M点时的速度大小 v= 
=2v0
竖直分速度 vy=v0cot30°= 
由h= 
，a= 
得
E= 
答：电场强度E的大小是 ．
（2）粒子进入磁场后由洛伦兹力充当向心力做匀速圆周运动，设轨迹半径为r．
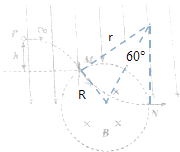
由牛顿第二定律得：qvB=m 
，r= 
= 
根据几何关系得：R=rtan30°= 
答：圆形区域的半径R是 ．
（3）在电场中，由h= 
得 t1= 
；
在磁场中，运动时间 t2= 
T= × 
= 
故带电粒子从P点到N点，所经历的时间 t=t1+t2= + ．
答：带电粒子从P点到N点，所经历的时间t是 + ．
【解析】(1)根据类平抛运动规律 ，利用带电粒子从M点射入磁场时，速度与竖直方向成30°角，求出竖直分速度，进而求出竖直方向的加速度，电场力提供加速度，再利用电场强度公式求出电场强度。
(2)高中物理求解带电粒子在电场中的圆周运动，一定会借助几何关系，第一步先画出运动轨迹，然后确定圆心，结合带电粒子在匀强电场半径公式最后借助几何关系求出半径。
(3)带电粒子从P点到N点，运动一共分成两段，在电场中的运动利用匀速直线运动公式可以求解，在磁场中，运动时间根据带电粒子运动时间公式求解。
【考点精析】利用洛伦兹力对题目进行判断即可得到答案，需要熟知洛伦兹力始终垂直于v的方向，所以洛伦兹力一定不做功．
