题目内容
19.在一次验证机械能守恒定律实验中,质量m=1kg 的重物自由下落,在纸带上打出一系列的点,如图1所示(打点间隔为0.02s),单位cm.那么
(1)打点计时器打下计数点B时,物体的速度vB=0.98m/s;
(2)从起点O到打下计数点B的过程中重力势能减少量是△Ep=0.49J.此过程中物体动能的增加量△Ek=0.48J(g取9.8m/s2);
(3)通过计算,数值上△Ep>△Ek(填“>”、“=”或“<”),这是因为重物和纸带下落时受到阻力作用;
(4)以各点到起始点的距离h为横坐标,以各点速度的平方v2为纵坐标建立直角坐标系,用实验测得的数据绘出v2-h图象,如图2所示:由v2-h图线求得重物下落的加速度g′=9.71m/s2.(结果保留三位有效数字)
分析 纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度,从而求出动能.根据功能关系得重力势能减小量等于重力做功的数值.
解答 解:(1)利用匀变速直线运动的推论有:
vB=$\frac{0.0706-0.0314}{2×0.02}$=0.98m/s
(2)重力势能减小量为:△Ep=mgh=1×9.8×0.0501J=0.49 J.
EkB=$\frac{1}{2}$mvB2═0.48 J.
(3)通过计算,数值上△Ep>△Ek,重物和纸带下落时受到阻力作用;
(4)由$\frac{1}{2}$mv2=mg′h可得:v2=2g′h,
由v2-h图线可求得:图线的斜率k=19.42
由k=2g′可得:物体下落的加速度g′=9.71 m/s2.
故答案为:(1)0.98 m/s
(2)0.49 J;0.48 J
(3)>,重物和纸带下落时受到阻力作用
(4)9.71
点评 要知道重物带动纸带下落过程中能量转化的过程和能量守恒,重物带动纸带下落过程中,除了重力还受到阻力,从能量转化的角度,由于阻力做功,重力势能减小除了转化给了动能还有一部分转化给摩擦产生的内能.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
10.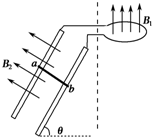 一个闭合回路由两部分组成,如图所示,右侧是电阻为r的圆形导线,置于竖直方向均匀变化的磁场B1中;左侧是光滑的倾角为θ的平行导轨,宽度为d,其电阻不计.磁感应强度为B2的匀强磁场垂直导轨平面向上,且只分布在虚线左侧,一个质量为m、电阻为R的导体棒此时恰好能静止在导轨上,下述判断正确的有( )
一个闭合回路由两部分组成,如图所示,右侧是电阻为r的圆形导线,置于竖直方向均匀变化的磁场B1中;左侧是光滑的倾角为θ的平行导轨,宽度为d,其电阻不计.磁感应强度为B2的匀强磁场垂直导轨平面向上,且只分布在虚线左侧,一个质量为m、电阻为R的导体棒此时恰好能静止在导轨上,下述判断正确的有( )
 一个闭合回路由两部分组成,如图所示,右侧是电阻为r的圆形导线,置于竖直方向均匀变化的磁场B1中;左侧是光滑的倾角为θ的平行导轨,宽度为d,其电阻不计.磁感应强度为B2的匀强磁场垂直导轨平面向上,且只分布在虚线左侧,一个质量为m、电阻为R的导体棒此时恰好能静止在导轨上,下述判断正确的有( )
一个闭合回路由两部分组成,如图所示,右侧是电阻为r的圆形导线,置于竖直方向均匀变化的磁场B1中;左侧是光滑的倾角为θ的平行导轨,宽度为d,其电阻不计.磁感应强度为B2的匀强磁场垂直导轨平面向上,且只分布在虚线左侧,一个质量为m、电阻为R的导体棒此时恰好能静止在导轨上,下述判断正确的有( )| A. | 圆形线圈中的磁场可以是向上均匀减弱 | |
| B. | 圆形导线中的电热功率为$\frac{{m}^{2}{g}^{2}si{n}^{2}θ}{{{B}_{2}}^{2}{d}^{2}}$(r+R) | |
| C. | 回路中的感应电流为$\frac{mgsinθ}{{B}_{2}d}$ | |
| D. | 导体棒ab受到的安培力大小为mgsinθ |
7. 如图所示,M是一小型理想变压器,接线柱a、b接在电压u=311sin 314t (V)的正弦交流电源上,变压器右侧部分为一火警报警系统原理图,其中R2是半导体热敏传感器(温度升高时R2的电阻减小),电流表A2安装在值班室,显示通过R1的电流,电压表V2显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时,以下说法中正确的是( )
如图所示,M是一小型理想变压器,接线柱a、b接在电压u=311sin 314t (V)的正弦交流电源上,变压器右侧部分为一火警报警系统原理图,其中R2是半导体热敏传感器(温度升高时R2的电阻减小),电流表A2安装在值班室,显示通过R1的电流,电压表V2显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时,以下说法中正确的是( )
 如图所示,M是一小型理想变压器,接线柱a、b接在电压u=311sin 314t (V)的正弦交流电源上,变压器右侧部分为一火警报警系统原理图,其中R2是半导体热敏传感器(温度升高时R2的电阻减小),电流表A2安装在值班室,显示通过R1的电流,电压表V2显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时,以下说法中正确的是( )
如图所示,M是一小型理想变压器,接线柱a、b接在电压u=311sin 314t (V)的正弦交流电源上,变压器右侧部分为一火警报警系统原理图,其中R2是半导体热敏传感器(温度升高时R2的电阻减小),电流表A2安装在值班室,显示通过R1的电流,电压表V2显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时,以下说法中正确的是( )| A. | A1的示数增大,A2的示数减小 | B. | A1的示数不变,A2的示数增大 | ||
| C. | V1的示数减小,V2的示数减小 | D. | V1的示数增大,V2的示数增大 |
14. 如图所示,传送带两轮间距为3m,不计轮的大小,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )
如图所示,传送带两轮间距为3m,不计轮的大小,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )
 如图所示,传送带两轮间距为3m,不计轮的大小,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )
如图所示,传送带两轮间距为3m,不计轮的大小,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )| A. | 摩擦力对物体做的功为4 J | B. | 摩擦力对物体做的功为-4 J | ||
| C. | 电动机做的功为8 J | D. | 电动机做功的功率为8 W |
4.下列说法正确的是( )
| A. | 物体没有功,则物体就没有能量 | |
| B. | 重力对物体做功,物体的重力势能一定减少 | |
| C. | 滑动摩擦力只能做负功 | |
| D. | 重力对物体做功,物体的重力势能可能增加 |
8.图甲是小型交流发电机的示意图,两磁极N、S间的磁场可视为水平方向的匀强磁场,?为交流电流表.线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动,从图示位置开始计时,产生的交变电流随时间变化的图象如图乙所示,以下判断不正确的是( )


| A. | 线圈转动的转速为50r/s | B. | 0.01s时,线圈平面与磁感线平行 | ||
| C. | 0.15s时,电流表的示数为0A | D. | 0.02s时,E点电势高于F点电势 |
9.冥王星与其附近的星体卡戎可视为双星系统,质量比约为7:1,同时绕它们连线上某点O做匀速圆周运动.由此可知冥王星绕O点运动的( )
| A. | 轨道半径约为卡戎的$\frac{1}{7}$ | B. | 角速度大小与卡戎的相同 | ||
| C. | 线速度大小约为卡戎的7倍 | D. | 向心力大小约为卡戎的7倍 |