题目内容
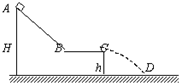
 如图所示,AB和BC是由相同材料组成的绝缘斜面和水平面,A与C的水平距离为SAC=5米,H高2.8米,h=0.8米.质量为m的小滑块由A静止开始释放,它恰能运动到C而静止.现在让小滑块带上电量q,并在轨道所在处施加竖直向下的匀强电场,场强大小E=mg/2q,在A点给小滑块一个沿斜面向下的4米/秒的初速度,求滑块滑出C后所抛出的水平距离是多大?
如图所示,AB和BC是由相同材料组成的绝缘斜面和水平面,A与C的水平距离为SAC=5米,H高2.8米,h=0.8米.质量为m的小滑块由A静止开始释放,它恰能运动到C而静止.现在让小滑块带上电量q,并在轨道所在处施加竖直向下的匀强电场,场强大小E=mg/2q,在A点给小滑块一个沿斜面向下的4米/秒的初速度,求滑块滑出C后所抛出的水平距离是多大?下面是一位同学对上述问题的求解:
未加电场小滑块由A静止下滑,由动能定理结合题意有:
mg(H-h)-μmgSAC=0(1)
加电场后,由动能定理结合题意有:
(mg+qE)(H-h)-μmgSAC=
| 1 |
| 2 |
联解方程(1)和(2)得:
v=
|
| g(H-h)+v02 |
小滑块离开C后作平抛运动:h=
| 1 |
| 2 |
结合题给条件和上述结果有:s=v
|
请你对这位同的求解作出评价:
(1)答案是否正确?简述正确与否的理由.
(2)如果你认为答案不正确,请完成该问题的求解过程,求出正确的答案.
分析:(1)本题有两种情况:不加电场与加电场,要分析物体的受力情况的变化,判断该同学的答案是否正确.
(2)对A到C的运动过程,运用动能定理对两种情况分别列式求物体到达C点的速度,再由平抛运动的规律求水平距离
(2)对A到C的运动过程,运用动能定理对两种情况分别列式求物体到达C点的速度,再由平抛运动的规律求水平距离
解答:解:(1)该同学的答案不正确.
原因在于在施加竖直向下的电场后,物体对桌面压力N=mg+qE,因而物体受到的滑动摩擦力f=μN=μ(mg+qE),而这位同学仍用f=μmg来计算摩擦力做的功.
(2)据上分析,仍保留这位同学列出的(1)式:mg(H-h)-μmgSAC=0
修改(2)式为:(mg+qE)(H-h)-μ(mg+qE)SABcosθ-μ(mg+qE)SBC=
m(υ2-
)
而SABcosθ+SBC=SAC.则得
(mg+qE)(H-h)-μ(mg+qE)SAC=
m(υ2-
)
联解上述两式得:υ=υ0=4米/秒
滑块滑出C后做平抛运动,运用平抛运动的公式:h=
gt2
得:S=vt=υ
=4×
m=1.6m
答:(1)该同学的答案不正确.原因在于在施加竖直向下的电场后,物体对桌面压力N=mg+qE,因而物体受到的滑动摩擦力f=μN=μ(mg+qE),而这位同学仍用f=μmg来计算摩擦力做的.
(2)正确的答案是:滑块滑出C后所抛出的水平距离为1.6m.
原因在于在施加竖直向下的电场后,物体对桌面压力N=mg+qE,因而物体受到的滑动摩擦力f=μN=μ(mg+qE),而这位同学仍用f=μmg来计算摩擦力做的功.
(2)据上分析,仍保留这位同学列出的(1)式:mg(H-h)-μmgSAC=0
修改(2)式为:(mg+qE)(H-h)-μ(mg+qE)SABcosθ-μ(mg+qE)SBC=
| 1 |
| 2 |
| υ | 2 0 |
而SABcosθ+SBC=SAC.则得
(mg+qE)(H-h)-μ(mg+qE)SAC=
| 1 |
| 2 |
| υ | 2 0 |
联解上述两式得:υ=υ0=4米/秒
滑块滑出C后做平抛运动,运用平抛运动的公式:h=
| 1 |
| 2 |
得:S=vt=υ
|
|
答:(1)该同学的答案不正确.原因在于在施加竖直向下的电场后,物体对桌面压力N=mg+qE,因而物体受到的滑动摩擦力f=μN=μ(mg+qE),而这位同学仍用f=μmg来计算摩擦力做的.
(2)正确的答案是:滑块滑出C后所抛出的水平距离为1.6m.
点评:本题是评价题,步骤要完整,先判断正误,后说明理由,再给出正确的解答,共有三步.运用动能定理时,仍需要分析受力情况,再确定做功情况.

练习册系列答案
相关题目
 如图所示,AB和BC是两段半径、长度及粗糙程度均相同的圆弧形路面,它们在B处相切平滑连在一起,且A、B、c在同一水平面上.一小物块以初速度v0从A端沿路面滑到C端时的速度大小为v1;而以同样大小的初速度v0从c端沿路面滑到A端时的速度大小为v2.则( )
如图所示,AB和BC是两段半径、长度及粗糙程度均相同的圆弧形路面,它们在B处相切平滑连在一起,且A、B、c在同一水平面上.一小物块以初速度v0从A端沿路面滑到C端时的速度大小为v1;而以同样大小的初速度v0从c端沿路面滑到A端时的速度大小为v2.则( )
 m(v2-v2) (2)
m(v2-v2) (2) =
=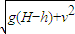 =6m/s
=6m/s gt2,s=vt,
gt2,s=vt, =2.4m
=2.4m