题目内容
17.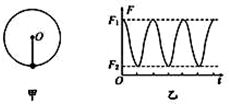 一宇航员到达半径为R、密度均匀的某星球表面,做如下实验:用不可伸长的轻绳拴一质量为m的小球,上端固定在O点,如图甲所示,在最低点给小球某一初速度,使其绕O点的竖直面内做圆周运动,测得绳的拉力F大小随时间t的变化规律如图乙所示.F1=7F2,设R、m、引力常量G以及F1为已知量,忽略各种阻力.以下说法正确是( )
一宇航员到达半径为R、密度均匀的某星球表面,做如下实验:用不可伸长的轻绳拴一质量为m的小球,上端固定在O点,如图甲所示,在最低点给小球某一初速度,使其绕O点的竖直面内做圆周运动,测得绳的拉力F大小随时间t的变化规律如图乙所示.F1=7F2,设R、m、引力常量G以及F1为已知量,忽略各种阻力.以下说法正确是( )| A. | 该星球表面的重力加速度为$\frac{F_2}{7m}$ | B. | 卫星绕该星球的第一宇宙速度为$\sqrt{\frac{Gm}{R}}$ | ||
| C. | 星球的质量为$\frac{{{F_1}{R^2}}}{7Gm}$ | D. | 小球在最高点的最小速度为零 |
分析 (1)对砝码受力分析,在最高点和最低点时,由向心力的公式和整个过程的机械能守恒可以求得重力加速度的大小;
(2)根据万有引力提供向心力可以求得星球的第一宇宙速度.
(3)求得星球表面的重力加速度的大小,再由在星球表面时,万有引力和重力近似相等,可以求得星球的质量;
(4)对小球在最高点运用牛顿第二定律分析求解问题.
解答 解:A、设砝码在最低点时细线的拉力为F1,速度为v1,则
F1-mg=m$\frac{{v}_{1}^{2}}{R}$…①
设砝码在最高点细线的拉力为F2,速度为v2,则
F2+mg=m$\frac{{v}_{2}^{2}}{R}$…②
由机械能守恒定律得 mg2r+$\frac{1}{2}$mV22=$\frac{1}{2}$mV12 …③
由①、②、③解得:
g=$\frac{{{F}_{1}-F}_{2}}{6m}$…④
F1=7F2,
所以该星球表面的重力加速度为$\frac{{F}_{2}}{m}$.故A错误.
B、根据万有引力提供向心力得:G$\frac{mM}{{R}^{2}}$=$\frac{{mv}^{2}}{R}$
卫星绕该星球的第一宇宙速度为v=$\sqrt{\frac{GM}{R}}$,故B错误.
C、在星球表面,万有引力近似等于重力
G$\frac{Mm′}{{R}^{2}}$=m′g…⑤
由④、⑤解得:M=$\frac{{{F_1}{R^2}}}{7Gm}$,故C正确.
D、小球在最高点受重力和绳子拉力,根据牛顿运动定律得:
F2+mg=m$\frac{{v}_{2}^{2}}{R}$≥mg
所以小球在最高点的最小速v2≥$\sqrt{gR}$.故D错误.
故选:C.
点评 根据做圆周运动时在最高点和最低点的运动规律,找出向心力的大小,可以求得重力加速度,
知道在星球表面时,万有引力和重力近似相等,而贴着星球的表面做圆周运动时,物体的重力就作为做圆周运动的向心力.

| A. | 一定做曲线运动 | B. | 一定做匀变速运动 | ||
| C. | 必沿F2反方向做直线运动 | D. | 必沿F2方向做直线运动 |
| A. | 卡文迪许通过实验测出了引力常量G | |
| B. | 惯性定律是可以被实验直接验证的 | |
| C. | 伽利略斜面实验合理外推解释了自由落体是匀变速运动 | |
| D. | 开普勒发现了行星运动的规律 |
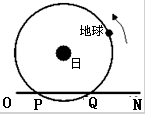 星际探测是现代航天科技发展的重要课题,我国将发射探测器进行星际探测.如图,某探测器从空间的O点沿直线ON从静止开始以加速度a作匀加速直线运动,两个月后与地球相遇于P点,再经两个月与地球相遇于Q点,已知引力常量G,地球公转周期为T(12个月),忽略所有天体对探测器的影响,把地球绕太阳的运动看做匀速圆周运动.根据上述信息,估算出:
星际探测是现代航天科技发展的重要课题,我国将发射探测器进行星际探测.如图,某探测器从空间的O点沿直线ON从静止开始以加速度a作匀加速直线运动,两个月后与地球相遇于P点,再经两个月与地球相遇于Q点,已知引力常量G,地球公转周期为T(12个月),忽略所有天体对探测器的影响,把地球绕太阳的运动看做匀速圆周运动.根据上述信息,估算出: 如图示,以9.8m/s的水平初速度抛出的物体,飞行一段时间后垂直的撞在倾角为30°的斜面上,物体空中飞行的时间为$\sqrt{3}$s. ( g取9.8m/s2)
如图示,以9.8m/s的水平初速度抛出的物体,飞行一段时间后垂直的撞在倾角为30°的斜面上,物体空中飞行的时间为$\sqrt{3}$s. ( g取9.8m/s2)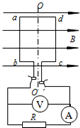 如图所示,交流发电机的矩形线圈abcd中,ab=cd=50cm,bc=ad=20cm,匝数n=100,线圈电阻r=0.2Ω,外电阻R=4.8Ω.线圈在磁感强度B=0.05$\sqrt{2}$T的匀强磁场中绕垂直于磁场的转轴OO′匀速转动,角速度ω=100πrad/s.求:
如图所示,交流发电机的矩形线圈abcd中,ab=cd=50cm,bc=ad=20cm,匝数n=100,线圈电阻r=0.2Ω,外电阻R=4.8Ω.线圈在磁感强度B=0.05$\sqrt{2}$T的匀强磁场中绕垂直于磁场的转轴OO′匀速转动,角速度ω=100πrad/s.求: 如图所示,水平台面AB距地面的高度h=0.80m.有一滑块从A点以v0=6.0m/s的初速度在台面上做匀变速直线运动,滑块与平台间的动摩擦因数μ=0.25.滑块运动到平台边缘的B点后水平飞出.已知AB=2.2m.不计空气阻力,g取10m/s2,求:
如图所示,水平台面AB距地面的高度h=0.80m.有一滑块从A点以v0=6.0m/s的初速度在台面上做匀变速直线运动,滑块与平台间的动摩擦因数μ=0.25.滑块运动到平台边缘的B点后水平飞出.已知AB=2.2m.不计空气阻力,g取10m/s2,求: