题目内容
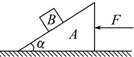（2003?肇庆模拟）如图所示，在水平面上有一质量为M的楔形木块A，其倾斜角为α，一质量为m的木块B放在A的斜面上．现对A施一水平推力F，使B与A不发生相对滑动，忽略一切摩擦，则B对A的压力大小为（ ）分析：B与A恰好不发生相对滑动时，B与A的加速度相同，以B为研究对象，根据牛顿第二定律可求出A对B的支持力．以AB整体为研究对象，根据牛顿第二定律求出加速度，再对B研究求出A对B的支持力，由牛顿第三定律得到B对A的压力大小．
解答：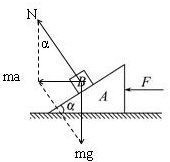
解：A、B以B木块为研究对象，B与A不发生相对滑动时，B的加速度水平向左，分析受力如图，根据牛顿第二定律得：
A对B的支持力为：N=
由牛顿第三定律得到：
B对A的压力大小为：N′=N=
．故A错误，B正确．
C、D以AB整体为研究对象，由牛顿第二定律得加速度为：a=
对B研究得有：N′=
=
．故C正确，D错误．
故选BC
解：A、B以B木块为研究对象，B与A不发生相对滑动时，B的加速度水平向左，分析受力如图，根据牛顿第二定律得：A对B的支持力为：N=
| mg |
| cosα |
由牛顿第三定律得到：
B对A的压力大小为：N′=N=
| mg |
| cosα |
C、D以AB整体为研究对象，由牛顿第二定律得加速度为：a=
| F |
| M+m |
对B研究得有：N′=
| ma |
| sinα |
| Fm |
| (M+m)sinα |
故选BC
点评：本题是连接类型的问题，两物体的加速度相同，既可以采用隔离法，也可以采用整体法和隔离法相结合的方法研究，要灵活选择研究对象，关键是不要漏选．
练习册系列答案
阅读快车系列答案
相关题目
（2003?肇庆模拟）用如图所示的装置进行以下实验：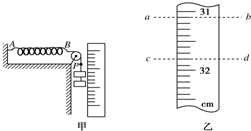
（2003?肇庆模拟）用如图甲所示的装置测定弹簧的劲度系数，被测弹簧一端固定于A点，另一端B用细绳绕过定滑轮挂钩码，旁边竖直固定一最小刻度为mm的刻度尺，当挂两个钩码时，绳上一定点P对应刻度如图乙中ab虚线所示，再增加一个钩码后，P点对应刻度如图乙中cd虚线所示，已知每个钩码质量为50g，重力加速度g=9.8m/s2，则被测弹簧的劲度系数为
（2003?肇庆模拟）一个质量m=0.20kg的小球系于轻质弹簧的一端，且套在光滑竖立的圆环上，弹簧的上端固定于环的最高点A，环的半径R=0.5m，弹簧的原长L0=0.50m，劲度系数为4.8N/m，如图所示，若小球从图中所示位置B点由静止开始滑动到最低点C时，弹簧的弹性势能Ep弹=0.60J．
（2003?肇庆模拟）在把电流表改装成电压表的实验中，测定电流表的内阻时，备有如下器材：