Question

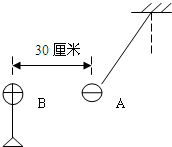
把质量为2.0克的带负电的小球A，用绝缘细绳悬挂起，若将带电量为Q=4.0×10^-6库的带电小球B靠近A，如图所示．当两个带电小球在同一高度相距30厘米时，绳与竖直方向恰成45°角．（AB可看成点电荷）求：
（l）A球受的库仑力；
（2）A球的带电量是多少？

Answer 1

分析：（1）对小球A受力分析，受到重力、静电引力和细线的拉力，根据三力平衡求出静电引力；
（2）根据库仑定律求解出小球A的带电量．

解答：解：（1）对球A受力分析，如图

根据共点力平衡条件，结合几何关系得到
Tsin45°=mg
Tcos45°=F
解得
F=mgtan45°=mg=0.02N
即A球受的库仑力为0.02N．
（2）根据库仑定律，有
F=k

qQ

r2

故
q=

Fr2

kQ

=

0.02×0.09

9×109×4×10-6

=5×10-8N
即A球的带电量是5×10^-8C．

点评：本题关键先根据平衡条件得到库仑力，再根据库仑定律求解出B球的带电量．