题目内容
一质点做匀加速直线运动,途径A、B、C三点,已知由A到B和由B到C所用时间均为t,位移分别为x1和x2,试证明:
(1)质点运动的加速度a=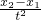 ;
;
(2)质点运动到达B点时的速度vB等于质点由A到C的平均速度vAC.
证明:(1)设A点的初速度为v0,则有:x1=v0t+ at2;
at2;
B点的速度vB=v0+at
x2=vBt+ at2;=v0t+
at2;=v0t+ at2;
at2;
x2-x1=at2
故a=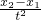
(2)由上可知:vB=v0+at
AC间的距离x=v0×2t+ a(2t)2=2v0t+2at2;
a(2t)2=2v0t+2at2;
AC段的平均速度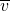 =
=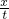 =v0+at
=v0+at
故vB=vAC,则可证明质点运动到达B点时的速度vB等于质点由A到C的平均速度vAC
分析:(1)分别对AB和BC列出位移公式,由位移公式可求得加速度的表达式;
(2)B点为AC段的中间时刻,由位移公式可得出平均速度与中间时刻速度的大小关系.
点评:本题所证两个结论在解题中经常用到,在平时要注意应用.
 at2;
at2;B点的速度vB=v0+at
x2=vBt+
 at2;=v0t+
at2;=v0t+ at2;
at2;x2-x1=at2
故a=
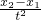
(2)由上可知:vB=v0+at
AC间的距离x=v0×2t+
 a(2t)2=2v0t+2at2;
a(2t)2=2v0t+2at2;AC段的平均速度
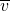 =
=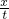 =v0+at
=v0+at故vB=vAC,则可证明质点运动到达B点时的速度vB等于质点由A到C的平均速度vAC
分析:(1)分别对AB和BC列出位移公式,由位移公式可求得加速度的表达式;
(2)B点为AC段的中间时刻,由位移公式可得出平均速度与中间时刻速度的大小关系.
点评:本题所证两个结论在解题中经常用到,在平时要注意应用.

练习册系列答案
相关题目
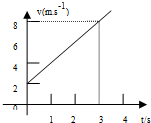 如图所示的速度图象表示一质点做匀加速直线运动,试根据图象带质点的初速度v0=
如图所示的速度图象表示一质点做匀加速直线运动,试根据图象带质点的初速度v0=