题目内容
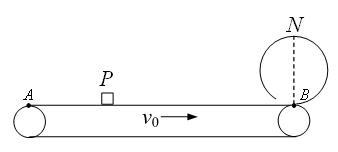
(20分)光滑水平面上有一质量为M="2" kg的足够长的木板,木板上最右端有一大小可忽略、质量为m=3kg的物块,物块与木板间的动摩擦因数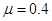 ,且最大静摩擦力等于滑动摩擦力。开始时物块和木板都静止,距木板左端L=2.4m处有一固定在水平面上的竖直弹性挡板P。现对物块施加一水平向左外力F=6N,若木板与挡板P发生撞击时间极短,并且搏击时无动能损失,物块始终未能与挡板相撞,求:
,且最大静摩擦力等于滑动摩擦力。开始时物块和木板都静止,距木板左端L=2.4m处有一固定在水平面上的竖直弹性挡板P。现对物块施加一水平向左外力F=6N,若木板与挡板P发生撞击时间极短,并且搏击时无动能损失,物块始终未能与挡板相撞,求:

(1)木板第一次撞击挡板P时的速度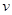 为多少?
为多少?
(2)木板从第一次撞击挡板P到运动到右端最远处所需的时间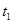 及此时物块距木板右端的距离X为多少?
及此时物块距木板右端的距离X为多少?
(3)木板与挡板P会发生多次撞击直至静止,而物块一直向左运动。每次木板与挡板p撞击前物块和木板都已相对静止,最后木板静止于挡板P处,求木板与物块都静止时物块距木板有端的距离X为多少?
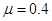 ,且最大静摩擦力等于滑动摩擦力。开始时物块和木板都静止,距木板左端L=2.4m处有一固定在水平面上的竖直弹性挡板P。现对物块施加一水平向左外力F=6N,若木板与挡板P发生撞击时间极短,并且搏击时无动能损失,物块始终未能与挡板相撞,求:
,且最大静摩擦力等于滑动摩擦力。开始时物块和木板都静止,距木板左端L=2.4m处有一固定在水平面上的竖直弹性挡板P。现对物块施加一水平向左外力F=6N,若木板与挡板P发生撞击时间极短,并且搏击时无动能损失,物块始终未能与挡板相撞,求:
(1)木板第一次撞击挡板P时的速度
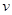 为多少?
为多少? (2)木板从第一次撞击挡板P到运动到右端最远处所需的时间
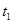 及此时物块距木板右端的距离X为多少?
及此时物块距木板右端的距离X为多少? (3)木板与挡板P会发生多次撞击直至静止,而物块一直向左运动。每次木板与挡板p撞击前物块和木板都已相对静止,最后木板静止于挡板P处,求木板与物块都静止时物块距木板有端的距离X为多少?
(1)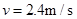 (2)
(2)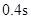
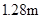 (3)
(3)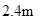
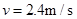 (2)
(2)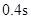
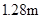 (3)
(3)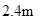
试题分析:(1)设木板靠最大静摩擦力或滑动摩擦力产生的加速度为
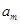 ,则
,则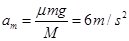 ①
① 若木板与物块不发生相对运动,设共同加速度为
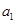 ,则
,则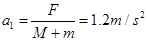 ②
② 因
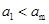 ,所以木板与物块靠静摩擦力一起以加速度a1运动 ③
,所以木板与物块靠静摩擦力一起以加速度a1运动 ③ 根据运动学公式
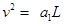 ④
④ 解得
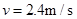 ⑤
⑤ (2)设木板第一次撞击挡板P后向右运动时,此时木板和物块之间摩擦力变为滑动摩擦力。
物块的加速度大小为
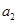 ,根据牛顿第二定律有
,根据牛顿第二定律有 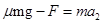 ⑥
⑥解得
 ⑦
⑦ 木板则以
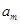 匀减速运动,因为
匀减速运动,因为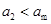 ,所以在木板向右减速运动过程中,物块一直向左减速,木板速度减为0时,木块仍在向左运动。设木板第一次撞击挡板P后运动到右端最远处所需时间为t1,则
,所以在木板向右减速运动过程中,物块一直向左减速,木板速度减为0时,木块仍在向左运动。设木板第一次撞击挡板P后运动到右端最远处所需时间为t1,则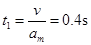 ⑧
⑧ 设木板左端距挡板P的距离为
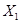 ,则
,则 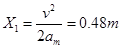 ⑨
⑨设物块相对地向左的位移为
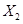 ,则
,则  ⑩
⑩ 此时物块距木板右端的距离
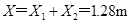 ⑾
⑾ (3)木板最终静止于挡板P处,设物块距木板右端的距离为
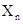 ,根据功能关系得
,根据功能关系得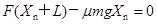 ⑿
⑿ 解得
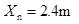 ⒀
⒀ 评分参考:第(1)问5分,①②③④⑤式各1分;第(2)问10分,其中⑥式2分,⑦式1分,⑧⑨⑩式各2分,⑾式1分;第(3)问5分,⑿式3分,⒀式2分。

练习册系列答案
相关题目

 )。试求:
)。试求:
