题目内容
如下图所示,在电视机显像管中的某区域同时加有磁感应强度相同的水平匀强磁场和竖直匀强磁场,磁场宽度为l,磁场右边界与荧光屏之间的距离也为l。质量为m、电荷量为e的电子经电压为U的电场加速后射入该磁场。在屏上建立坐标系,x、y轴分别沿水平、竖直方向。若不加磁场时,电子打在坐标原点O。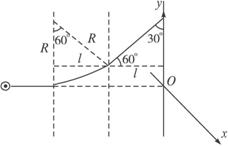
(1)若只加水平方向的磁场,则打到屏上时速度方向与竖直方向成30°角,求打在屏上落点的坐标。
(2)只加水平方向的磁场时,求磁感应强度和电子在磁场中运动的时间。
(3)若同时加上两个方向的匀强磁场,求电子在屏上的落点到坐标原点O的距离。
解:(1)如图所示,电子做匀速圆周运动的半径

R=![]()
电子偏离竖直方向的距离
y=R-Rcos60°+lcot30°
联立解得y=![]() l,所求坐标(0,
l,所求坐标(0,![]() l)。
l)。
(2)对电子由动能定理:eU=![]() mv02
mv02
设磁场的磁感应强度为B,ev0B=m![]()
联立解出B=![]()
时间t=![]() T
T
又T=![]()
联立解出t=![]() 。
。
(3)若只加竖直方向的匀强磁场,
同理可求出电子偏离水平方向的距离x=![]() l
l
故所求为S=![]() l。
l。

练习册系列答案
相关题目
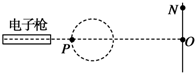
 电视机显像管中,电子束的偏转是用磁偏转技术实现的,在电子枪中产生的电子经过加速电场加速后射出,从P点进入并通过圆形区域后,打到荧光屏上,如下图所示.如果圆形区域中不加磁场,电子一直打到荧光屏上的中心O点的动能为E;在圆形区域内加垂直于圆面、磁感应强度为B的匀强磁场后,电子将打到荧光屏的上端N点.已知ON=h,PO=L.电子的电荷量为e,质量m.求
电视机显像管中,电子束的偏转是用磁偏转技术实现的,在电子枪中产生的电子经过加速电场加速后射出,从P点进入并通过圆形区域后,打到荧光屏上,如下图所示.如果圆形区域中不加磁场,电子一直打到荧光屏上的中心O点的动能为E;在圆形区域内加垂直于圆面、磁感应强度为B的匀强磁场后,电子将打到荧光屏的上端N点.已知ON=h,PO=L.电子的电荷量为e,质量m.求