题目内容
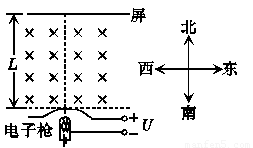
电视机显像管中,电子束的偏转是用磁偏转技术实现的,在电子枪中产生的电子经过加速电场加速后射出,从P点进入并通过圆形区域后,打到荧光屏上,如下图所示.如果圆形区域中不加磁场,电子一直打到荧光屏上的中心O点的动能为E;在圆形区域内加垂直于圆面、磁感应强度为B的匀强磁场后,电子将打到荧光屏的上端N点.已知ON=h,PO=L.电子的电荷量为e,质量为m.求(1)电子打到荧光屏上的N点时的动能是多少?说明理由;
(2)电子在电子枪中加速的加速电压是多少?
(3)电子在磁场中做圆周运动的半径R是多少?

【答案】分析:(1)电子经过偏转磁场时洛伦兹力不做功,可知电子打到荧光屏上的N点时的动能仍为E.
(2)根据动能定理求解电子在电子枪中加速的加速电压.
(3)电子在磁场中由洛伦兹力提供向心力而做圆周运动,根据牛顿第二定律求解圆周运动的半径.
解答:解:(1)电子经过偏转磁场时洛伦兹力不做功,根据动能定理可知,电子打到荧光屏上的N点时的动能仍为E.
(2)根据动能定理得:eU=E,得U=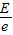
(3)电子在磁场中由洛伦兹力提供向心力而做圆周运动,根据牛顿第二定律得
evB=m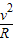
得,R=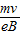
又E=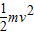
解得,R=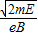
答:(1)电子打到荧光屏上的N点时的动能是E,因为电子经过偏转磁场时洛伦兹力不做功.
(2)电子在电子枪中加速的加速电压是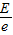 .
.
(3)电子在磁场中做圆周运动的半径R是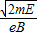 .
.
点评:本题根据动能定理求解加速获得的速度,电子在磁场中由洛伦兹力提供向心力,求解半径,都是常用的方法,难度不大.
(2)根据动能定理求解电子在电子枪中加速的加速电压.
(3)电子在磁场中由洛伦兹力提供向心力而做圆周运动,根据牛顿第二定律求解圆周运动的半径.
解答:解:(1)电子经过偏转磁场时洛伦兹力不做功,根据动能定理可知,电子打到荧光屏上的N点时的动能仍为E.
(2)根据动能定理得:eU=E,得U=
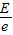
(3)电子在磁场中由洛伦兹力提供向心力而做圆周运动,根据牛顿第二定律得
evB=m
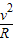
得,R=
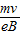
又E=
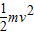
解得,R=
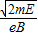
答:(1)电子打到荧光屏上的N点时的动能是E,因为电子经过偏转磁场时洛伦兹力不做功.
(2)电子在电子枪中加速的加速电压是
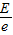 .
.(3)电子在磁场中做圆周运动的半径R是
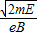 .
.点评:本题根据动能定理求解加速获得的速度,电子在磁场中由洛伦兹力提供向心力,求解半径,都是常用的方法,难度不大.

练习册系列答案
相关题目
 电视机显像管中,电子束的偏转是用磁偏转技术实现的,在电子枪中产生的电子经过加速电场加速后射出,从P点进入并通过圆形区域后,打到荧光屏上,如下图所示.如果圆形区域中不加磁场,电子一直打到荧光屏上的中心O点的动能为E;在圆形区域内加垂直于圆面、磁感应强度为B的匀强磁场后,电子将打到荧光屏的上端N点.已知ON=h,PO=L.电子的电荷量为e,质量m.求
电视机显像管中,电子束的偏转是用磁偏转技术实现的,在电子枪中产生的电子经过加速电场加速后射出,从P点进入并通过圆形区域后,打到荧光屏上,如下图所示.如果圆形区域中不加磁场,电子一直打到荧光屏上的中心O点的动能为E;在圆形区域内加垂直于圆面、磁感应强度为B的匀强磁场后,电子将打到荧光屏的上端N点.已知ON=h,PO=L.电子的电荷量为e,质量m.求 电视机显像管中需要用变化的磁场来控制电子束的偏转.图甲为显像管工作原理示意图,阴极K发射的电子束(初速不计)经电压为U的电场加速后,进入一圆形匀强磁场区,磁场方向垂直于圆面(以垂直圆面向里为正方向),磁场区的中心为O,半径为r,荧光屏MN到磁场区中心O的距离为L.当不加磁场时,电子束将通过O点垂直打到屏幕的中心P点.当磁场的磁感应强度随时间按图乙所示的规律变化时,在荧光屏上得到一条长为
电视机显像管中需要用变化的磁场来控制电子束的偏转.图甲为显像管工作原理示意图,阴极K发射的电子束(初速不计)经电压为U的电场加速后,进入一圆形匀强磁场区,磁场方向垂直于圆面(以垂直圆面向里为正方向),磁场区的中心为O,半径为r,荧光屏MN到磁场区中心O的距离为L.当不加磁场时,电子束将通过O点垂直打到屏幕的中心P点.当磁场的磁感应强度随时间按图乙所示的规律变化时,在荧光屏上得到一条长为