Question

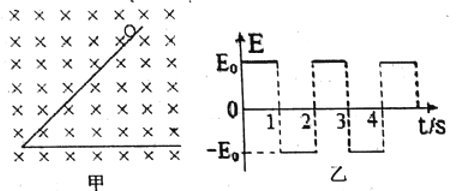
【题目】在如图甲所示的空间内，存在垂直纸面向里的匀强磁场，磁感应强度为。在竖直方向存在交替变化的匀强电场(取竖直向上为正)，场强大小，如图乙所示。一倾角为、长度足够长的光滑绝缘斜面放置在此空间，斜面上有一质量为m，带电量为-q的甲小球，从t=0时刻由静止开始沿斜面下滑，设第5s内甲小球不会离开斜面，重力加速度为g.求:

(1)在5s内斜面对甲小球的最大支持力及电场力对小球做的功:

(2)第6s内甲小球离开斜面的最大距离;

(3)在第6s内甲小球离开斜面的距离最大时，让电场强度方向不再变化，同时撤去光滑斜面，在甲小球斜下方的A点射入另一个质量也为m、带电量为q的乙小球。设A点与此时甲小球相距为x、它们的连线与原斜面垂直，乙小球与此时甲小球速度大小相等、方向相反。此后两小球间可能发生的碰撞都是完全弹性碰撞，而且电量也不会转移，忽略两小球间的电作用力。在以后的运动过程中甲小球能通过A点求x的所有可能值。

Answer 1

【答案】(1) 2mgcosθ；9mg2sin2θ(2)(3) ；

【解析】

（1）在5s内斜面对小球的最大支持力是在t＝0时，大小为2mgcosθ，设第一秒内小球在斜面上运动的加速度为a，由牛顿第二定律得：

（mg+qE0）sinθ=ma

在第二秒内：

qE0=mg

所以小球将离开斜面在上方做匀速圆周运动，

圆周运动的周期为：

故小球在奇数秒内沿斜面做匀加速运动，在偶数秒内离开斜面做完整的圆周运动

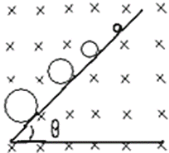
小球在5s内沿斜面通过的位移：

电场力做功：

W电=E0qxsinθ

代入数据解得：

W电=9mg2sin2θ

（2）第五秒末的速度为：

v5＝a(t1＋t3＋t5)＝6gsinθ

接着做匀速圆周运动，由向心力公式得：

qv5B=m

小球离开斜面的最大距离为：

d＝2R3

所以此最大距离为：

（3）第五秒末的速度为：

v5＝a(t1＋t3＋t5)＝6gsinθ

接着做匀速圆周运动，由向心力公式得：

qv5B=m

甲小球离开斜面的最大距离为：

d＝2R3

乙小球与甲小球碰撞是完全弹性碰撞，所以碰撞后两球速度交换，因此，两小球在碰撞后均做半径为R3的匀速圆周运动。有二种情况甲小球能通过A点。

第一种情况如图（a）所示，两球未发生碰撞，甲小球转过半圈后到达A点，所以

第二种情况

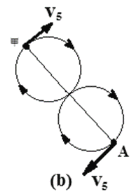
如图（b）所示，两球各自转过半圈后相碰，并交换速度，以后甲小球转半圈后到达A点，所以：