题目内容
20.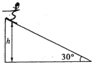 如图所示,某段滑雪雪道倾角为30°,总质量为m的滑雪运动员从距底端高为h处的雪道上由静止开始匀加速下滑,加速度为$\frac{1}{3}$g运动员从上向下滑到底端的过程中( )
如图所示,某段滑雪雪道倾角为30°,总质量为m的滑雪运动员从距底端高为h处的雪道上由静止开始匀加速下滑,加速度为$\frac{1}{3}$g运动员从上向下滑到底端的过程中( )| A. | 合外力做功为$\frac{1}{3}$mgh | B. | 增加的动能为$\frac{2}{3}$mgh | ||
| C. | 克服摩擦力做功为$\frac{1}{3}$mgh | D. | 减少的机械能为$\frac{1}{6}$mgh |
分析 本题中合外力做功由功的公式和牛顿第二定律结合即可求解;根据动能定理可求出动能的增加量;根据牛顿第二定律求出摩擦力大小,再根据功的公式即可求解克服摩擦力做功;根据“功能原理”求出减少的机械能.
解答 解:A、根据功的公式可知,合外力做功应为:W合=F合•$\frac{h}{sin30°}$=ma•2h=$\frac{2}{3}$mgh,故A错误;
B、对滑雪运动员,由动能定理可知,△Ek=W合=$\frac{2}{3}$mgh,故B正确;
C、对滑雪运动员由牛顿第二定律应有:mgsin30°-f=ma,可得运动员受到的阻力f=$\frac{1}{6}$mg,所以运动员克服摩擦力做的功为 Wf=f•$\frac{h}{sin30°}$=$\frac{1}{3}$mgh,故C正确;
D、根据“功能原理”可知减少的机械能应等于克服阻力做的功,即有:△E=Wf=$\frac{1}{3}$mgh,故D错误;
故选:BC
点评 本题应明确:①涉及到“动能”、“功”等字眼时考虑应用动能定理求解;②“功能原理”是指除重力以外其它力做的功等于物体机械能的变化.

练习册系列答案
相关题目
8. 如图,用恒力F拉着三个物体在光滑的水平面上一起运动.现在中间物体上加上一个小物体,那么连接物体的绳子张力和未放小物体前相比( )
如图,用恒力F拉着三个物体在光滑的水平面上一起运动.现在中间物体上加上一个小物体,那么连接物体的绳子张力和未放小物体前相比( )
 如图,用恒力F拉着三个物体在光滑的水平面上一起运动.现在中间物体上加上一个小物体,那么连接物体的绳子张力和未放小物体前相比( )
如图,用恒力F拉着三个物体在光滑的水平面上一起运动.现在中间物体上加上一个小物体,那么连接物体的绳子张力和未放小物体前相比( )| A. | Ta变小 | B. | Ta变大 | C. | Tb减小 | D. | Tb不变 |
15. 如图,将小砝码至于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,这就是大家熟悉的惯性演示实验.若砝码和纸板的质量分别为M和m,各接触面间的动摩擦因数均为μ,砝码与纸板左端的距离及桌面右端的距离均为d.现用水平向右的恒定拉力F拉动纸板,下列说法正确的是( )
如图,将小砝码至于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,这就是大家熟悉的惯性演示实验.若砝码和纸板的质量分别为M和m,各接触面间的动摩擦因数均为μ,砝码与纸板左端的距离及桌面右端的距离均为d.现用水平向右的恒定拉力F拉动纸板,下列说法正确的是( )
 如图,将小砝码至于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,这就是大家熟悉的惯性演示实验.若砝码和纸板的质量分别为M和m,各接触面间的动摩擦因数均为μ,砝码与纸板左端的距离及桌面右端的距离均为d.现用水平向右的恒定拉力F拉动纸板,下列说法正确的是( )
如图,将小砝码至于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,这就是大家熟悉的惯性演示实验.若砝码和纸板的质量分别为M和m,各接触面间的动摩擦因数均为μ,砝码与纸板左端的距离及桌面右端的距离均为d.现用水平向右的恒定拉力F拉动纸板,下列说法正确的是( )| A. | 纸板相对砝码运动时,纸板所受摩擦力的大小为μ(M+m)g | |
| B. | 要使纸板相对砝码运动,F一定大于2μ(M+m)g | |
| C. | 若砝码与纸板分离时的速度小于$\sqrt{μgd}$,砝码不会从桌面上掉下 | |
| D. | 当F=μ(2M+4m)g时,砝码恰好到达桌面边缘 |
9. 如图所示,三个相同的小球从同一高度处的O点分别以水平初速度v1、v2、v3抛出,落在水平面上的位置分别是A、B、C,O′是O在水平面上的射影点,若不计空气阻力,则下列说法正确的是( )
如图所示,三个相同的小球从同一高度处的O点分别以水平初速度v1、v2、v3抛出,落在水平面上的位置分别是A、B、C,O′是O在水平面上的射影点,若不计空气阻力,则下列说法正确的是( )
 如图所示,三个相同的小球从同一高度处的O点分别以水平初速度v1、v2、v3抛出,落在水平面上的位置分别是A、B、C,O′是O在水平面上的射影点,若不计空气阻力,则下列说法正确的是( )
如图所示,三个相同的小球从同一高度处的O点分别以水平初速度v1、v2、v3抛出,落在水平面上的位置分别是A、B、C,O′是O在水平面上的射影点,若不计空气阻力,则下列说法正确的是( )| A. | 三小球动能改变量相同 | |
| B. | 三个小球落地时的速度大小相同,但方向不同 | |
| C. | 落地时C小球速度与水平方向夹角最小 | |
| D. | 三个小球落地的动能相同 |
10.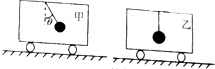 如图所示,在平直轨道上甲、乙两车均作直线运动,其内各自用不可伸长的轻质细线悬挂一个小球,甲中的悬线与竖直方向保持恒定的夹角θ,乙中的悬线保持竖直,则有关甲、乙两车运动情况及小球受力情况,下列说法正确的是( )
如图所示,在平直轨道上甲、乙两车均作直线运动,其内各自用不可伸长的轻质细线悬挂一个小球,甲中的悬线与竖直方向保持恒定的夹角θ,乙中的悬线保持竖直,则有关甲、乙两车运动情况及小球受力情况,下列说法正确的是( )
 如图所示,在平直轨道上甲、乙两车均作直线运动,其内各自用不可伸长的轻质细线悬挂一个小球,甲中的悬线与竖直方向保持恒定的夹角θ,乙中的悬线保持竖直,则有关甲、乙两车运动情况及小球受力情况,下列说法正确的是( )
如图所示,在平直轨道上甲、乙两车均作直线运动,其内各自用不可伸长的轻质细线悬挂一个小球,甲中的悬线与竖直方向保持恒定的夹角θ,乙中的悬线保持竖直,则有关甲、乙两车运动情况及小球受力情况,下列说法正确的是( )| A. | 甲小车一定向左作匀加速运动 | |
| B. | 甲小车一定具有方向向左的加速度 | |
| C. | 甲车中小球受到绳子的拉力一定大于其重力 | |
| D. | 乙小车一定作匀速运动 |
 如图所示的传送带以速率v=2m/s匀速运行,AB部分水平,BC部分与水平面之间的夹角为30°,AB间与BC间距离都等于12m,工件与传送带间的动摩擦因数为μ=$\frac{\sqrt{3}}{6}$,现将质量为5kg的工件轻轻放在传送带的A端,假设工件始终没有离开传送带,g取10m/s2,求:工件滑至C点时的速度大小.
如图所示的传送带以速率v=2m/s匀速运行,AB部分水平,BC部分与水平面之间的夹角为30°,AB间与BC间距离都等于12m,工件与传送带间的动摩擦因数为μ=$\frac{\sqrt{3}}{6}$,现将质量为5kg的工件轻轻放在传送带的A端,假设工件始终没有离开传送带,g取10m/s2,求:工件滑至C点时的速度大小.
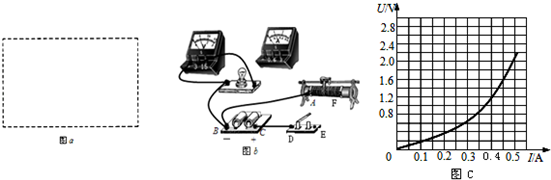
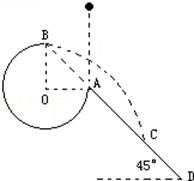 如图所示,竖直平面内的$\frac{3}{4}$圆弧形光滑轨道半径为R,A端与圆心O等高,AD为与水平方向成45°角的斜面.B端在O的正上方.一个小球在A点正上方由静止开始释放,自由下落至A点后进入圆形轨道并恰能到达B点,求:
如图所示,竖直平面内的$\frac{3}{4}$圆弧形光滑轨道半径为R,A端与圆心O等高,AD为与水平方向成45°角的斜面.B端在O的正上方.一个小球在A点正上方由静止开始释放,自由下落至A点后进入圆形轨道并恰能到达B点,求: