��Ŀ����
2�� ��ͼ��ʾ���ڻ�����ľ�ǹ��֮����һС���Ǵ�����������Ǵ��е�С����ֻ�ܵ�̫��������������̫��������Բ���˶�������˵������ȷ���ǣ�������
��ͼ��ʾ���ڻ�����ľ�ǹ��֮����һС���Ǵ�����������Ǵ��е�С����ֻ�ܵ�̫��������������̫��������Բ���˶�������˵������ȷ���ǣ�������| A�� | ��С������̫���˶�������С��һ�� | |
| B�� | С���Ǵ��ڲ����ǵļ��ٶ�С��������ǵļ��ٶ� | |
| C�� | С���Ǵ��ڸ�������̫����ת�����ٶȾ�С�ڵ�����̫����ת�����ٶ� | |
| D�� | ��̫��������ȵ�ÿһ��С���ǣ��ܵ�̫����������С����� |
���� �о�������̫��������Բ���˶����������������ṩ���������г���ʽ��ʾ�����ڡ����ٶȡ�����������������
���ݹ���뾶�Ĺ�ϵ�жϸ��������Ĵ�С��ϵ��
��� �⣺A���������������ṩ�������ã�
$\frac{GMm}{{r}^{2}}$=m$\frac{{4��}^{2}}{{T}^{2}}$r
T=2��$\sqrt{\frac{{r}^{3}}{GM}}$
��̫��ԽԶ������Խ�����Ը�С������̫���˶������ڴ��ڵ���Ĺ�ת���ڣ���A����
B���������������ṩ�������ã�$\frac{GMm}{{r}^{2}}$=ma
a=$\frac{GM}{{r}^{2}}$������С���Ǵ��ڲ�С���ǵ����ļ��ٶȴ������С���ǵ����ļ��ٶ�ֵ����B����
C���������������ṩ�������ã�
$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$
v=$\sqrt{\frac{GM}{r}}$
����С���Ǵ��ڸ�С����Բ���˶������ٶ�ֵС�ڵ���ת�����ٶ�ֵ����C��ȷ��
D����ΪС���ǵ�������һ����ͬ����̫���Ը�С���ǵ�������һ����ͬ����D����
��ѡ��C��
���� �Ƚ�һ��������������Ӧ�ð����������������֪����������ʾ�������ٽ��бȽϣ�
�������Ĺ�ʽѡȡҪ������Ŀ�ṩ����֪��������������������ѡȡӦ�ã�

 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
| A�� | ��������֧��������Ħ������������������ | |
| B�� | Ħ�����ķ�����˶��켣������ | |
| C�� | ������֧������һ���������ͷ�������������� | |
| D�� | Ħ������ʹ����������Բ���˶��������� |
 ��ͼ��ʾ��С��ͬѧ���������ϲ����У��Ⱦ�ֹ�����ڵ����ϣ�Ȼ�������������������������ж���ȷ���ǣ�������
��ͼ��ʾ��С��ͬѧ���������ϲ����У��Ⱦ�ֹ�����ڵ����ϣ�Ȼ�������������������������ж���ȷ���ǣ�������| A�� | ��ֹ����ʱ������֮�������ͼʾλ�������ֱ۵��������� | |
| B�� | ��ֹ�����ڵ�����ʱ��С������ʧ��״̬ | |
| C�� | ��������������ʱ�����ܶ��˲����� | |
| D�� | ��������������ʱ�����ܶ��������� |
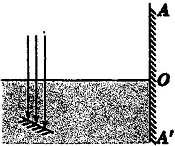 ��ͼ��ʾ�����ⴹֱ���뾲ֹ��ˮ�У�ˮ����ǽ�㹻Զ��ij����һСƽ�澵����ǽOA��OA���ϸ���һ��߷ֱ�ΪS��S�䣨ͼ��δ������������֪ˮ�Ժ��������Ϊn1�����Ϲ�������Ϊn2��ƽ�澵��ˮƽ��ļн�Ϊ�ȣ�����˵����ȷ���ǣ�������
��ͼ��ʾ�����ⴹֱ���뾲ֹ��ˮ�У�ˮ����ǽ�㹻Զ��ij����һСƽ�澵����ǽOA��OA���ϸ���һ��߷ֱ�ΪS��S�䣨ͼ��δ������������֪ˮ�Ժ��������Ϊn1�����Ϲ�������Ϊn2��ƽ�澵��ˮƽ��ļн�Ϊ�ȣ�����˵����ȷ���ǣ�������| A�� | ���S�Dz�ɫ�����ϱ�Ե����ɫ | |
| B�� | ������ȣ����S��������ʧ���Ǻ�� | |
| C�� | ����֤S��S������ڣ�����sin2�ȣ�$\frac{1}{{n}_{1}}$ | |
| D�� | ����֤S��S������ڣ�����sin$\frac{��}{2}$��$\frac{1}{{n}_{2}}$ |
 ����ѡ��һ���Ӵ�A������糡����B��������糡�ĵ���������ӵ��˶��켣��ͼ��ʾ��ͼ�����ǰ����������˴�ƽ�еȾ࣬�������ڵĵ��������Ʋ���ȣ��������ӵ�����������˵����ȷ���� ��������
����ѡ��һ���Ӵ�A������糡����B��������糡�ĵ���������ӵ��˶��켣��ͼ��ʾ��ͼ�����ǰ����������˴�ƽ�еȾ࣬�������ڵĵ��������Ʋ���ȣ��������ӵ�����������˵����ȷ���� ��������| A�� | ���Ӵ������ | B�� | ���ӵļ��ٶ��Ȳ��䣬���С | ||
| C�� | ���ӵ��ٶȲ������� | D�� | ���ӵĵ������ȼ�С�������� |
 ��ͼ��ʾ������ˮƽ�����ϵ�ľ��A���ھ�ֹ״̬�����ҵ���������̵�������Ϊ0.6kg�����ɲ����ƶ���Ϊ2N������Ħ�����ƣ�������ȡ�����еIJ������룬ʹ��������С��0.3kg��������ֵ�����ǣ�ȡg=10m/s2����������
��ͼ��ʾ������ˮƽ�����ϵ�ľ��A���ھ�ֹ״̬�����ҵ���������̵�������Ϊ0.6kg�����ɲ����ƶ���Ϊ2N������Ħ�����ƣ�������ȡ�����еIJ������룬ʹ��������С��0.3kg��������ֵ�����ǣ�ȡg=10m/s2����������| A�� | ���ɲ����ƵĶ�������С | B�� | A�������˶� | ||
| C�� | A���ܵ�Ħ��������С3 N | D�� | A���ܵĺ�����Ҫ��� |
 ��һ������Ϊm��������Ϊ-q�����ӣ��������ƣ�����Ϊ��ɣ�Χ��һ��������Ϊ+Q�ĵ�����Բ���˶�����ͼ����֪�˶��뾶ΪR����
��һ������Ϊm��������Ϊ-q�����ӣ��������ƣ�����Ϊ��ɣ�Χ��һ��������Ϊ+Q�ĵ�����Բ���˶�����ͼ����֪�˶��뾶ΪR���� ��ͼ��ʾ�ǹ̶�����ֱƽ���ڵİ뾶R=0.9m�İ�Բ�����һ����Ϊm��С���ع���ڲ��˶��պ��ܹ���ߵ㣮����С���뿪�������ص�����Բ���ڵ�����ͶӰ��֮��ľ��룮��g=10m/s2��
��ͼ��ʾ�ǹ̶�����ֱƽ���ڵİ뾶R=0.9m�İ�Բ�����һ����Ϊm��С���ع���ڲ��˶��պ��ܹ���ߵ㣮����С���뿪�������ص�����Բ���ڵ�����ͶӰ��֮��ľ��룮��g=10m/s2�� ��ͼ��ʾ��������ľ�ԵС����A������R=0.4m�ľ�Եϸ����ֱ���ң�����O��ˮƽ����ĸ߶�Ϊ3R��С����B�����磮λ��O�����·��ĵ����ϣ���L=2R�ľ�Եˮƽ���ʹ��ϱ�������ĸ߶�h=2R���������O����ͬһ��ֱ���ϣ��Ҷ˵��Ҳ�ռ��з�����ֱ���µ���ǿ�糡���ڣ����봫�ʹ�֮����λ�ÿɵ��Ĺ̶����ӣ�ͼ��δ������������A����ˮƽλ���ɾ�ֹ�ͷź������赲��ϸ���ܻ���ѣ�ʹ��A�ܻ��ϴ��ʹ������˶��������ʹ���ʱ������ת����A�պ����˶������ʹ����Ҷˣ���֪��Եϸ���ܳ��ܵ����������A������5����A���ܵ糡����С��������ȣ��������ٶ�g=10m/s2��A��B������Ϊ�ʵ㣬Ƥ�������ְ뾶��С��A�����������Ѷ���ʧ������Ҳ������Ħ������ʧ�������
��ͼ��ʾ��������ľ�ԵС����A������R=0.4m�ľ�Եϸ����ֱ���ң�����O��ˮƽ����ĸ߶�Ϊ3R��С����B�����磮λ��O�����·��ĵ����ϣ���L=2R�ľ�Եˮƽ���ʹ��ϱ�������ĸ߶�h=2R���������O����ͬһ��ֱ���ϣ��Ҷ˵��Ҳ�ռ��з�����ֱ���µ���ǿ�糡���ڣ����봫�ʹ�֮����λ�ÿɵ��Ĺ̶����ӣ�ͼ��δ������������A����ˮƽλ���ɾ�ֹ�ͷź������赲��ϸ���ܻ���ѣ�ʹ��A�ܻ��ϴ��ʹ������˶��������ʹ���ʱ������ת����A�պ����˶������ʹ����Ҷˣ���֪��Եϸ���ܳ��ܵ����������A������5����A���ܵ糡����С��������ȣ��������ٶ�g=10m/s2��A��B������Ϊ�ʵ㣬Ƥ�������ְ뾶��С��A�����������Ѷ���ʧ������Ҳ������Ħ������ʧ�������