Question

【题目】如图所示，直角三角形MPN区域内存在着垂直纸面向外的匀强磁场，其中MP=d，MNP=。，AB是一段电阻丝，预热后能产生大量无初速度的自由电子，电阻丝的B端位于NP的连线上，AB与BN垂直，在AB与MP间存在水平向左的匀强电场。调整电阻丝AB到MP的距离，发现从MP中点进入磁场的电子恰好垂直MN边射出，且电子在磁场中运动的时间为t。 已知电子的质量为m，电荷量为e，不计电子重力及电子间相互作用力，求：

(1)应强度B的大小；

(2)调整电阻丝AB到MP的距离，发现有些电子能在MN边上相遇，若相遇的两电子在磁场中运动的时间之差的最大值为2t。，则满足此条件的电子速度的最大值为多少？

Answer 1

【答案】(1)(2)

【解析】

(1)电子垂直于MN边射出,轨迹如图所示，

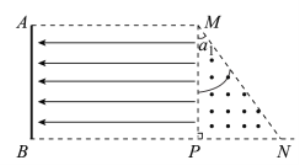
圆心O与M点重合,圆心角,半径，洛伦兹力提供向心力有

电子做圆周运动的周期

电子的运动时间

联立解得

(2)若两个电子在MN上相交于C点,轨迹如图所示,

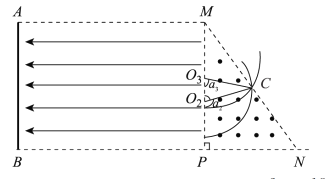
三角形CO2O3为等腰三角形,由图可知其圆心角分别为和，且有

所用时间之差

要让为最大值,需要为最大的角,即轨迹应与MN相切,轨迹如图所示

当时,有

解得

由图可知,在所有和MN相切的圆里,只有半径最大时,电子的速度最大。即电子应从P点射人且和MN相切,速度才最大

解得

由牛顿第二定律得：

解得