Question

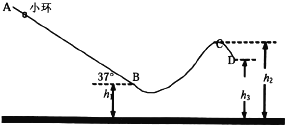
【题目】如图，AB为粗糙的长直轨道，与水平方向的夹角为37°，BCD为光滑曲线轨道，两段轨道在B处光滑连接。B、C、D三点离水平地面的高度分别为h1＝1m，h2＝1.8m和h3＝1.55m。一质量m＝0.2kg的小环套在轨道AB上，由静止开始释放，经过t＝1.5s到达B点，速度vB＝6m/s。求：（sin37°＝06，cos37°＝0.8，g取10m/s2）

（1）小环沿AB运动的加速度a的大小；

（2）小环沿AB运动时所受摩擦力Ff的大小；

（3）小环离开轨道D处时的速度vD的大小；

（4）若使小环以最小速度落地，求小环在AB上释放处离地的高度h。

Answer 1

【答案】（1）4m/s2；（2）0.4N；（3）5m/s；（4）2.2m。

【解析】

（1）小环从A到B做初速度为零的匀加速直线运动，由加速度的定义式求加速度a。

（2）分析小环受力，由牛顿第二定律求摩擦力Ff的大小；

（3）BCD为光滑曲线轨道，小环从B到D只有重力做功，其机械能守恒，由机械能守恒定律求小环离开轨道D处时的速度vD的大小；

（4）若使小环以最小速度落地，则小环在C点的瞬时速度为零。由机械能守恒定律求出B点的速度，再由运动学公式求小环在AB上释放处离地的高度h。

（1）小环从A到B做初速度为零的匀加速直线运动，加速度为：

a＝＝4m/s2。

（2）小环在AB段受力情况如图所示。由牛顿第二定律得：

mgsin37°﹣Ff＝ma

解得：Ff＝0.4N

（3）小环从B到D运动过程中只有重力做功，其机械能守恒，则有：

mgh1+＝mgh3+

解得：vD＝5m/s

（4）若使小环以最小速度落地，则小环在C点的瞬时速度为零。小环从B到C运动过程中只有重力做功，其机械能守恒。由机械能守恒定律得：

mgh1+＝mgh2+

解得：vB′＝4m/s

小环从释放处到B作初速度为零的匀加速直线运动，位移为：

s＝m＝2m

根据几何关系得：h＝h1+ssin37°

解得：h＝2.2m。