题目内容
如图10所示,宽度 、足够长的平行此光滑金属导轨固定在位于竖直平面内的绝缘板上,导轨所在空间存在磁感应强度B=0.50T的匀强磁场,磁场方向跟导轨所在平面垂直。一根导体棒MN两端套在导轨上与导轨接触良好,且可自由滑动,导体棒的电阻值R=l.5Ω,其他电阻均可忽略不计。电源电动势E=3.0V,内阻可忽略不计,重力加速度g取10m/s2。当S1闭合,S2断开时,导体棒恰好静止不动。
、足够长的平行此光滑金属导轨固定在位于竖直平面内的绝缘板上,导轨所在空间存在磁感应强度B=0.50T的匀强磁场,磁场方向跟导轨所在平面垂直。一根导体棒MN两端套在导轨上与导轨接触良好,且可自由滑动,导体棒的电阻值R=l.5Ω,其他电阻均可忽略不计。电源电动势E=3.0V,内阻可忽略不计,重力加速度g取10m/s2。当S1闭合,S2断开时,导体棒恰好静止不动。

(1)求S1闭合,S2断开时,导体棒所受安培力的大小;
(2)将S1断开,S2闭合,使导体棒由静止开始运动,求当导体棒的加速度 =5.0m/s2时,导体棒产生感应电动势的大小;
=5.0m/s2时,导体棒产生感应电动势的大小;
(3)将S1断开,S2闭合,使导体棒由静止开始运动,求导体棒运动的最大速度的大小。
 、足够长的平行此光滑金属导轨固定在位于竖直平面内的绝缘板上,导轨所在空间存在磁感应强度B=0.50T的匀强磁场,磁场方向跟导轨所在平面垂直。一根导体棒MN两端套在导轨上与导轨接触良好,且可自由滑动,导体棒的电阻值R=l.5Ω,其他电阻均可忽略不计。电源电动势E=3.0V,内阻可忽略不计,重力加速度g取10m/s2。当S1闭合,S2断开时,导体棒恰好静止不动。
、足够长的平行此光滑金属导轨固定在位于竖直平面内的绝缘板上,导轨所在空间存在磁感应强度B=0.50T的匀强磁场,磁场方向跟导轨所在平面垂直。一根导体棒MN两端套在导轨上与导轨接触良好,且可自由滑动,导体棒的电阻值R=l.5Ω,其他电阻均可忽略不计。电源电动势E=3.0V,内阻可忽略不计,重力加速度g取10m/s2。当S1闭合,S2断开时,导体棒恰好静止不动。
(1)求S1闭合,S2断开时,导体棒所受安培力的大小;
(2)将S1断开,S2闭合,使导体棒由静止开始运动,求当导体棒的加速度
 =5.0m/s2时,导体棒产生感应电动势的大小;
=5.0m/s2时,导体棒产生感应电动势的大小;(3)将S1断开,S2闭合,使导体棒由静止开始运动,求导体棒运动的最大速度的大小。
(1)F1=0.20N (2)E1=1.5V (3)vm=30m/s
(1)当S1闭合,S2断开时,
导体棒静止,通过导体棒的电流
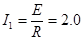 A ………………………2分
A ………………………2分
此时导体棒所受安培力 F1=BI1L=0.20N……2分
(2)当S1闭合,S2断开时,导体棒静止,
有G=F1=0.20N…………………………………2分
设S1断开,S2闭合的情况下,导体棒加速度a=5.0m/s2时,其所受安培力为F2,速度为v1,通过导体棒的电流为I2,导体棒产生的感应电动势为E1。
根据牛顿第二定律有G-F2=ma,解得F2=0.10N…………………2分
由F2=BI2L,解得I2=1.0A…………………………………2分
根据欧姆定律有E1= I2R,解得E1=1.5V……………………2分
(3)将S1断开,S2闭合,导体棒由静止开始运动,当导体棒所受重力与安培力平衡时,导体棒的速度达到最大,设最大速度为vm。……………2分
所以有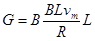 ,解得
,解得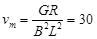 m/s……………2分
m/s……………2分
导体棒静止,通过导体棒的电流
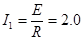 A ………………………2分
A ………………………2分此时导体棒所受安培力 F1=BI1L=0.20N……2分
(2)当S1闭合,S2断开时,导体棒静止,
有G=F1=0.20N…………………………………2分
设S1断开,S2闭合的情况下,导体棒加速度a=5.0m/s2时,其所受安培力为F2,速度为v1,通过导体棒的电流为I2,导体棒产生的感应电动势为E1。
根据牛顿第二定律有G-F2=ma,解得F2=0.10N…………………2分
由F2=BI2L,解得I2=1.0A…………………………………2分
根据欧姆定律有E1= I2R,解得E1=1.5V……………………2分
(3)将S1断开,S2闭合,导体棒由静止开始运动,当导体棒所受重力与安培力平衡时,导体棒的速度达到最大,设最大速度为vm。……………2分
所以有
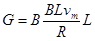 ,解得
,解得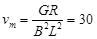 m/s……………2分
m/s……………2分
练习册系列答案
相关题目








