题目内容
13.宇航员站在一星球表面上某高度处沿水平方向抛出一个小球,经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L;若仅将抛出时的高度变为原来的2倍,则抛出与落地点之间的距离变为3L.已知两落地点在同一水平面上,设此星球半径为R,万有引力常量为G,求:(1)抛出时的初速度;
(2)该星球的密度.
分析 (1)小球在星球上做平抛运动,设表面的重力加速度为g,对两次平抛运动应用平抛运动基本公式列式,联立方程即可求解;
(2)求出重力加速度,再结合金代换GM=gR2可求的星球质量,再根据密度等于质量除以体积求解.
解答 解:(1)小球在星球上做平抛运动,设表面的重力加速度为g,第一次平抛的水平位移和竖直高度分别为x1和y1,第二次平抛的水平位移和竖直高度分别为x2和y2,
所以有:x1=v0t,
${y_1}=\frac{1}{2}g{t^2}$,
可得:${x_1}={v_0}\sqrt{\frac{{2{y_1}}}{g}}$,
可知今将高度变为原来的2倍时,${x_2}=\sqrt{2}{x_1}$,
由几何知识可得:$x_1^2+y_1^2={L^2}$,
${x}_{2}^{2}+{y}_{2}^{2}={(3L)}^{2}$,
即$2{x}_{1}^{2}+4{y}_{1}^{2}=9{L}^{2}$,
解得:${x_1}=\frac{L}{{\sqrt{2}}}$,${y_1}=\frac{L}{{\sqrt{2}}}$,
所以有:${v_0}=\frac{L}{{\sqrt{2}t}}$
(2)利用上式可得:$g=\frac{{\sqrt{2}L}}{t^2}$,
由黄金代换GM=gR2可得:$M=\frac{{\sqrt{2}L{R^2}}}{{G{t^2}}}$,
则密度为:$ρ=\frac{M}{V}=\frac{M}{\frac{4π}{3}{R}^{3}}=\frac{3\sqrt{2}L}{4πG{t}^{2}R}$.
答:(1)抛出时的初速度为$\frac{L}{\sqrt{2}t}$;
(2)该星球的密度为$\frac{3\sqrt{2}L}{4πG{t}^{2}R}$.
点评 本题提供了利用重力加速度估测星球质量的一种方法,利用平抛运动的分位移和合位移关系公式计算出重力加速度是关键.

| A. | 物体做匀速圆周运动时,合力提供向心力 | |
| B. | 物体只有受到一个方向时刻改变的力的作用才可能做曲线运动 | |
| C. | 物体在一恒力作用下不可能做曲线运动 | |
| D. | 曲线运动都是变速运动 |
| A. | 到达底部时重力的功率相等 | B. | 到达底部时速度相等 | ||
| C. | 下滑过程中重力做的功相等 | D. | 到达底部的时间相等 |
| A. | 物体在赤道处受的地球引力等于两极处,而重力小于两极处 | |
| B. | 赤道处的角速度比南纬30°的大 | |
| C. | 地球上物体的向心加速度都指向地心,且赤道上物体的向心加速度比两极处大 | |
| D. | 地面上的物体随地球自转时由万有引力的一个分力提供向心力 |
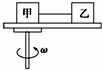 一圆盘可以绕其竖直轴在水平面内转动,圆盘半径为R,甲、乙两物体的质量分别为M与m(M>m),它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用一根长为l(l<R)的轻绳连在一起,如图,甲物体放在转动轴的位置上,甲、乙之间的连线刚好沿半径方向拉直,要使两物体与圆盘之间不发生相对滑动,则圆盘旋转的角速度最大值不得超过( )
一圆盘可以绕其竖直轴在水平面内转动,圆盘半径为R,甲、乙两物体的质量分别为M与m(M>m),它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用一根长为l(l<R)的轻绳连在一起,如图,甲物体放在转动轴的位置上,甲、乙之间的连线刚好沿半径方向拉直,要使两物体与圆盘之间不发生相对滑动,则圆盘旋转的角速度最大值不得超过( )| A. | $\sqrt{\frac{μ(M-m)g}{ml}}$ | B. | $\sqrt{\frac{μ(M-m)g}{Ml}}$ | C. | $\sqrt{\frac{μ(M+m)g}{Ml}}$ | D. | $\sqrt{\frac{μ(M+m)g}{ml}}$ |
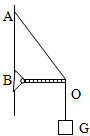 城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂,如图是这类结果的简化模型.图中轻杆OB可以绕过B点且垂直于纸面的轴转动,钢索OA和杆OB的质量都可以忽略不计,如果悬挂物的重力为G,∠ABO=90°,AB>OB,在某次产品质量检测和性能测试中保持A、B两点不动,只缓慢改变钢索OA的长度,则关于钢索OA的拉力F1和杆OB上的支持力F2的变化情况,下列说法正确的是( )
城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂,如图是这类结果的简化模型.图中轻杆OB可以绕过B点且垂直于纸面的轴转动,钢索OA和杆OB的质量都可以忽略不计,如果悬挂物的重力为G,∠ABO=90°,AB>OB,在某次产品质量检测和性能测试中保持A、B两点不动,只缓慢改变钢索OA的长度,则关于钢索OA的拉力F1和杆OB上的支持力F2的变化情况,下列说法正确的是( )| A. | 从图示位置开始缩短钢索OA,钢索OA的拉力F1先减小后增大 | |
| B. | 从图示位置开始缩短钢索OA,杆OB上的支持力F2不变 | |
| C. | 从图示位置开始伸长钢索OA,钢索OA的拉力F1增大 | |
| D. | 从图示位置开始伸长钢索OA,杆OB上的支持力F2先减小后增大 |
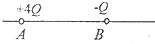 相距为L的电荷A、B的带电量分别为+4Q和-Q,将它们固定在光滑的水平面上,现引入第三个点电荷C,使C在库仑力作用下处于平衡状态,试分析C的带电量和放置的位置.若在引入点电荷C的时候,将点电荷A、B也释放,要使三个点电荷在库仑力作用下都处于平衡状态,试求C电荷的电量和放置的位置.
相距为L的电荷A、B的带电量分别为+4Q和-Q,将它们固定在光滑的水平面上,现引入第三个点电荷C,使C在库仑力作用下处于平衡状态,试分析C的带电量和放置的位置.若在引入点电荷C的时候,将点电荷A、B也释放,要使三个点电荷在库仑力作用下都处于平衡状态,试求C电荷的电量和放置的位置.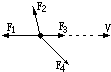 如图所示,质量为m的物体受到4个共点力的作用下正在作匀速直线运动,速度方向与F1、F3方向恰在一直线上,则(运动前填“直线”或“曲线”)
如图所示,质量为m的物体受到4个共点力的作用下正在作匀速直线运动,速度方向与F1、F3方向恰在一直线上,则(运动前填“直线”或“曲线”)