题目内容
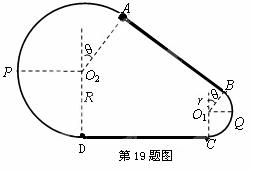
如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为L＝3m，圆弧形轨道APD和BQC均光滑，AB、CD与两圆弧形轨道相切，BQC的半径为r＝1m，APD的半径为R=2m， O2A、O1B与竖直方向的夹角均为q＝37°。现有一质量为m＝1kg的小球穿在滑轨上，以Ek0的初动能从B点开始沿AB向上运动，小球与两段直轨道间的动摩擦因数均为μ＝
，设小球经过轨道连接处均无能量损失。（g＝10m/s2，sin37°＝0.6，cos37°＝0.8）求：
（1）要使小球能够通过弧形轨道APD的最高点，初动能EK0至少多大？
（2）求小球第二次到达D点时的动能；
（3）小球在CD段上运动的总路程。（第（2）（3）两问中的EK0取第（1）问中的数值）
解析：（1）小球至少需要越过弧形轨道APD的最高点，根据动能定理：
……（2分）
代入 解得Ek0＝30J…………（2分）
（2）从B点出发到小球第一次回到B点的过程中，根据动能定理：
……（1分） 解得：EkB= 12J
小球沿AB向上运动到最高点，距离B点为s，则有：EkB=mmgscosq+mgssinq，……（2分）
解得s=18/13 （m）…（1分）
小球继续向下运动，当小球第
二次到达D点时动能为EKD，
……（1分）
解得：
J ……（2分）
（3）小球第二次到D点后还剩12.6J的能量，沿DP弧上升后再返回DC段，到C点只剩下2.6J的能量。因此小球无法继续上升到B点，滑到BQC某处后开始下滑，之后受摩擦力作用，小球最终停在CD上的某点。（1分）
由动能定理： 
…………（2分）解得：s1＝3.78m
小球通过CD段的总路程为S总＝2L＋s＝9.78m…………（1分）
名校课堂系列答案
（2011?江苏模拟）如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中水平直轨AB与倾斜直轨CD长均为L=6m，圆弧形轨道AQC和BPD均光滑，AQC的半径为r=1m，AB、CD与两圆弧形轨道相切，O2D、O1C与竖直方向的夹角均为θ=37°．现有一质量为m=1kg的小球穿在滑轨上，以Ek0=24J的初动能从B点开始水平向左运动，小球与两段直轨道间的动摩擦因数均为μ=
（2010?上海模拟）如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为L=3m，圆弧形轨道APD和BQC均光滑，BQC的半径为r=1m，APD的半径为R=2m，AB、CD与两圆弧形轨道相切，O2A、O1B与竖直方向的夹角均为θ=37°．现有一质量为m=1kg的小球穿在滑轨上，以Ek0的初动能从B点开始沿AB向上运动，小球与两段直轨道间的动摩擦因数均为μ=
如图所示为放置在竖直平面内游戏滑轨的模拟装置图，滑轨由四部分粗细均匀的金属杆组成，其中水平直轨AB与倾斜直轨CD两者的长L均为6m，圆弧形轨道AQC和BPD均光滑，AQC的半径r=1m，AB、CD与两圆弧形轨道相切，O2D、O1C与竖直方向的夹角θ均为37°．现有一质量m=1kg的小球穿在滑轨上，以30J的初动能Ek0从B点开始水平向右运动，小球与两段直轨道间的动摩擦因素μ均为
如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为L=3m，圆弧形轨道APD和BQC均光滑，BQC的半径为r=1m，APD的半径为R=2m，AB、CD与两圆弧形轨道相切，O2A、O1B与竖直方向的夹角均为θ=37°．现有一质量为m=1kg的小球穿在滑轨上，以初动能Ek0从B点开始沿BA向上运动，小球与两段直轨道间的动摩擦因数均为μ=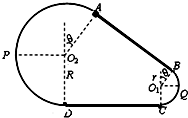
（2011?浙江模拟）如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为L=3m，圆弧形轨道APD和BQC均光滑，BQC的半径为r=1m，APD的半径为R，AB、CD与两圆弧形轨道相切，O2A、O1B与竖直方向的夹角均为θ=370．现有一质量为m=1kg的小环穿在滑轨上，以某一初速度从B点开始沿AB向上运动，并恰能通过滑轨最高点．设小环与两段直轨道间的动摩擦因数均为