Question

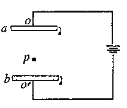
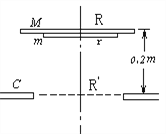
【题目】有两块大小不同的圆形薄板（厚度不计），质量分别为M和m，半径分别为R和，两板之间用一根长为0.4米的轻绳相连接。开始时，两板水平放置并叠合在一起，在其正下方0.2米处有一固定支架C，支架上有一半径为R’（ r< R’<R）的圆孔， 圆孔与两薄板的中心均在同一竖直线上，如图所示，让两个圆形薄板自由落下，落到固定支架上，大板与支架发生没有机械能损失的碰撞，碰撞后两板即分离，直到轻绳绷紧，在轻绳绷紧瞬间，两薄板具有共同速度vp，若M=m，则vp多大？

Answer 1

【答案】1m/s，方向向下

【解析】开始M与m自由下落，由械能守恒定律得：（M+m）gh=（M+m）v02，
代入数据解得：v0=2m/s；
M碰撞支架后以V0返回作竖直上抛运动，m继续下落做匀加速运动．经时间t，M上升高度为h1，m下落高度为h2．则：
h1=v0t- gt2h2=v0t+gt2
则h1+h2=2V0t=0.4m
代入数据解得：t=0.1s
设绳绷紧前M速度为V1，m的速度为V2，有：

v1=v0-gt=2-10×0.1=1m/s，v2=v0+gt=2+10×0.1=3m/s
绳绷紧时，取向下为正方向，根据动量守恒定律得：mv2-Mv1=（M+m）v
代入数据解得：v=1m/s；