题目内容
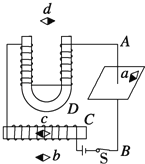
【题目】如图所示,ABCD为固定在竖直平面内的轨道,AB段光滑水平,BC段为光滑圆弧,对应的圆心角
θ=37°,半径r=2.5m,CD段平直倾斜粗糙且足够长,各段轨道均平滑连接,倾斜轨道所在区域有场强
大小为E=2×l05N/C、方向垂直于斜轨向下的匀强电场.质量m=2×l0﹣2kg、电荷量q=+1×10﹣6C的小物
体a被弹簧枪发射后,沿水平轨道向左滑行并与质量相等的不带电小物体b碰后粘在一起成带电体p
(视为质点)向左运动,并在C点以速度v0=3m/s冲上斜轨.以带电体p通过C点时为计时起点,0.1s
以后,场强大小不变,方向反向.已知斜轨与p间的动摩擦因数μ=0.2.设p的电荷量保持不变,取
g=10m/s2.sin37°=0.6,cos37°=0.8.(结果保留两位有效数字)

(1)求弹簧枪对小物体a所做的功;
(2)在斜轨上带电体p能到达的最高点为Q,求CQ的长度.
【答案】(1)0.76J (2)0.61m
【解析】试题分析:设弹簧枪对小物体做功为Wf,由动能定理即可求解;对小物体进行受力析,分析物体的运动情况,根据牛顿第二定律求出加速度,结合运动学基本公式即可求解。
(1)设弹簧枪对小物体做功为Wf,小物体a碰到b前的速度为v1,碰后整体P的共同速度为v2,由功能关系得: ![]()
由动量守恒得:mv1=2mv2
p机械能守恒得:![]()
联立以上解得:Wf=0.76J
(2)取沿平直斜轨向上为正方向.设带电体p通过C点进入电场后的加速度为a1,
由牛顿第二定律得:﹣2mgsinθ﹣μ(2mgcosθ+qE)=2ma1
p向上做匀减速运动,经t1=0.1s后,仍有向上速度达到v3,有:v3=v0+a1t1
由以上解得:v3=2.14m/s
设运动的位移为x1,根据位移与时间关系有:![]()
解得:x1=0.26m
电场力反向后,设小物体的加速度为a2,由牛顿第二定律得:
﹣2mgsinθ﹣μ(2mgcosθ﹣qE)=2ma2
设小物体以此加速度运动到速度为0,位移为x2,有:
根据速度与位移关系:2a2x2=v32
代入数据解得:x2=0.35m
设CE的长度为x,有:x=x1+x2
联立相关方程,代人数据解得:x=0.61m