题目内容
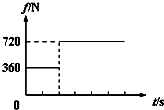 质量为60kg的消防队员从一根固定的、高度为6m的竖直金属杆顶端由静止滑下,消防队员受到的竖直向上的摩擦力变化情况如图所示(消防员视为质点).在消防队员下滑的过程中:
质量为60kg的消防队员从一根固定的、高度为6m的竖直金属杆顶端由静止滑下,消防队员受到的竖直向上的摩擦力变化情况如图所示(消防员视为质点).在消防队员下滑的过程中:(1)他刚开始下滑的加速度大小为多大?
(2)为了保证他落地时的速度为零,他应加速多长时间?整个下滑过程他克服摩擦力做的功是多少?
分析:(1)根据牛顿第二定律求出消防员刚开始下滑时的加速度大小.
(2)抓住匀减速直线运动和匀减速直线运动的位移之和等于金属杆的长度,求出加速运动的时间.对全过程运用动能定理求出下滑过程中克服摩擦力做功的大小.
(2)抓住匀减速直线运动和匀减速直线运动的位移之和等于金属杆的长度,求出加速运动的时间.对全过程运用动能定理求出下滑过程中克服摩擦力做功的大小.
解答:解:(1)根据牛顿第二定律得,消防员下滑的加速度a=
=
m/s2=4m/s2.
(2)匀减速直线运动的加速度大小a′=
=
m/s2=2m/s2.
设加速的时间为t.
匀加速直线运动的位移x1=
at2=2t2,
最大速度v=at=4t.
匀减速直线运动的位移x2=
=
=4t2
根据h=x1+x2,代入数据解得t=1s.
对全过程运用动能定理得,mgh-Wf=0
解得Wf=mgh=600×6J=3600J.
答:(1)他刚开始下滑的加速度大小为4m/s2.
(2)加速的时间为1s,整个下滑过程他克服摩擦力做的功是3600J.
| mg-f1 |
| m |
| 600-360 |
| 60 |
(2)匀减速直线运动的加速度大小a′=
| f′-mg |
| m |
| 720-600 |
| 60 |
设加速的时间为t.
匀加速直线运动的位移x1=
| 1 |
| 2 |
最大速度v=at=4t.
匀减速直线运动的位移x2=
| v2 |
| 2a′ |
| 16t2 |
| 4 |
根据h=x1+x2,代入数据解得t=1s.
对全过程运用动能定理得,mgh-Wf=0
解得Wf=mgh=600×6J=3600J.
答:(1)他刚开始下滑的加速度大小为4m/s2.
(2)加速的时间为1s,整个下滑过程他克服摩擦力做的功是3600J.
点评:本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系前后的桥梁.对于求解克服摩擦力做功问题,由于两段过程摩擦力大小不等,所以运用动能定理解决比较方便.

练习册系列答案
相关题目
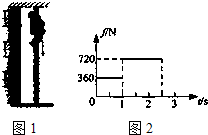 如图1所示,质量为60kg的消防队员从一根固定的竖直金属杆上由静止滑下,经过2.5s时间落到地面上.下滑中消防队员受到的竖直向上的摩擦力随时间变化的情况如图2所示,取g=10m/s2.求:
如图1所示,质量为60kg的消防队员从一根固定的竖直金属杆上由静止滑下,经过2.5s时间落到地面上.下滑中消防队员受到的竖直向上的摩擦力随时间变化的情况如图2所示,取g=10m/s2.求: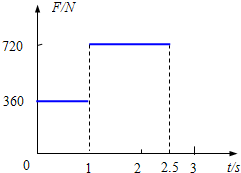 (2010?渭南一模)质量为60kg的消防队员,从一根竖直的长直轻绳上由静止滑下,经2.5s落地.轻绳上端有一力传感器,它记录的轻绳受到的拉力变化情况如图甲所地,取g=10m/s2.下列说法中正确的是( )
(2010?渭南一模)质量为60kg的消防队员,从一根竖直的长直轻绳上由静止滑下,经2.5s落地.轻绳上端有一力传感器,它记录的轻绳受到的拉力变化情况如图甲所地,取g=10m/s2.下列说法中正确的是( )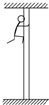 如图所示,长为12m的钢管沿着竖直方向固定在地面上.一名质量为60kg的消防队员在演习训练中,从钢管顶端由静止开始先匀加速再匀减速下滑,滑到地面时速度恰好为零.如果他加速时的加速度大小是减速时的2倍,下滑的总时间为3s,g 取10m/s2.关于消防队员在下滑的过程中,下列说法正确的是( )
如图所示,长为12m的钢管沿着竖直方向固定在地面上.一名质量为60kg的消防队员在演习训练中,从钢管顶端由静止开始先匀加速再匀减速下滑,滑到地面时速度恰好为零.如果他加速时的加速度大小是减速时的2倍,下滑的总时间为3s,g 取10m/s2.关于消防队员在下滑的过程中,下列说法正确的是( )