Question

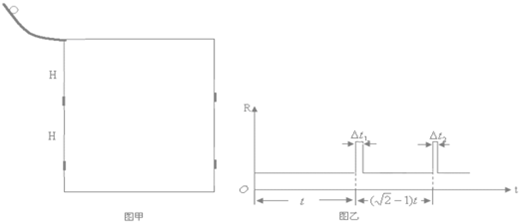
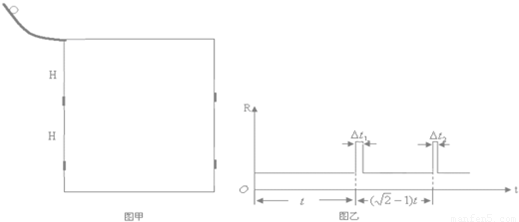
如图甲所示，在一对平行光滑的金属导轨的上端连接一阻值为R＝4 Ω的定值电阻，两导轨在同一平面内．质量为m＝0.1 kg，长为L＝0.1 m的导体棒ab垂直于导轨，使其从靠近电阻处由静止开始下滑，已知导体棒电阻为r＝1 Ω，整个装置处于垂直于导轨平面的匀强磁场中，导体棒下滑过程中加速度a与速度v的关系如图乙所示．(g＝10 m/s²)．求：

1.导轨平面与水平面间夹角θ；

2.磁场的磁感应强度B；

3.若靠近电阻处到底端距离为20 m，

ab棒在下滑至底端前速度已达10 m/s，

 求ab棒下滑的整个过程中，电阻R上产生的焦耳热．

 

Answer 1

 

1.即θ＝30°

2.B=5 T

3.Q_R ＝4J

解析:（1）依图可知，当ab棒静止时，a＝5 m/s^2，

此时对ab棒：mgsinθ＝m a     ①

               解得sinθ＝0.5 即θ＝30°

（2）依图可知，当ab棒速度v= 10 m/s 时，a＝0即

                            mgsinθ =F_安       ②

    又       ③

回路中的电流   ④

解上式得B=5 T

(3) 由能量守恒定律知，ab棒下滑的整个过程中,回路中产生的热量等于ab棒机械能的减少量即       Q= mgHsinθ－ ＝5J    ⑤

又Q=Q_R+Q_r       ⑥

⑦

Q_R ：Q_r＝R:r    ⑧

解上式得Q_R ＝4J