题目内容
 质量为m的机车头拖着质量均为m的n节车厢在平直轨道上以速度v匀速行驶,设机车头和各节车厢受到的阻力均为f,行驶中后面有一节车厢脱落,待脱落车厢停止运动时后面又有一节车厢脱落,各节车厢按此方式依次脱落,整个过程中机车头的牵引力保持不变,问:
质量为m的机车头拖着质量均为m的n节车厢在平直轨道上以速度v匀速行驶,设机车头和各节车厢受到的阻力均为f,行驶中后面有一节车厢脱落,待脱落车厢停止运动时后面又有一节车厢脱落,各节车厢按此方式依次脱落,整个过程中机车头的牵引力保持不变,问:(1)最后面一节车厢脱落后,机车头和剩下的车厢的加速度是多大?
(2)最后面一节车厢脱落后,当它停止运动时,机车头和剩下的车厢的速度是多大?
(3)全部车厢脱落并停止运动时,机车头的速度是多大?
分析:(1)最后面一节车厢脱落后,根据牛顿第二定律求解机车头和剩下的车厢的加速度.
(2)根据速度公式求出最后面一节车厢从脱落到停止运动的时间,再求解机车头和剩下的车厢的速度.
(3)采用同样的方法求出第二节车厢脱离、第三节车厢脱离…等等停止运动时,机车头和剩下的车厢的速度,总结规律,得出全部车厢脱落并停止运动时,机车头的速度.
(2)根据速度公式求出最后面一节车厢从脱落到停止运动的时间,再求解机车头和剩下的车厢的速度.
(3)采用同样的方法求出第二节车厢脱离、第三节车厢脱离…等等停止运动时,机车头和剩下的车厢的速度,总结规律,得出全部车厢脱落并停止运动时,机车头的速度.
解答:解:(1)最后面一节车厢脱落后,根据牛顿第二定律得
机车头和剩下的车厢的加速度a1=
又由匀速运动时,F=(n+1)f,得
a1=
(2)最后面一节车厢脱落后,加速度大小为a′=
最后面一节车厢从脱落到停止运动的时间为t1=
=
,
则当它停止运动时,机车头和剩下的车厢的速度v1=v+a1t1=v+
?
=
v
(3)第二节车厢脱离:
v2=v1+a2t2=v1+
?
=
=
第三节车厢脱离:
v3=v2+a3t3=v2+
?
=
=
…
同理可得:vn=
=
答:
(1)最后面一节车厢脱落后,机车头和剩下的车厢的加速度是
.
(2)最后面一节车厢脱落后,当它停止运动时,机车头和剩下的车厢的速度是
v.
(3)全部车厢脱落并停止运动时,机车头的速度是
.
机车头和剩下的车厢的加速度a1=
| F-nf |
| nm |
又由匀速运动时,F=(n+1)f,得
a1=
| f |
| nm |
(2)最后面一节车厢脱落后,加速度大小为a′=
| f |
| m |
最后面一节车厢从脱落到停止运动的时间为t1=
| v |
| a′ |
| mv |
| f |
则当它停止运动时,机车头和剩下的车厢的速度v1=v+a1t1=v+
| f |
| nm |
| mv |
| f |
| 1+n |
| n |
(3)第二节车厢脱离:
v2=v1+a2t2=v1+
| 2f |
| (n-1)m |
| mv1 |
| f |
| (1+n)v1 |
| n-1 |
| (1+n)2v |
| n(n-1) |
第三节车厢脱离:
v3=v2+a3t3=v2+
| 3f |
| (n-2)m |
| mv2 |
| f |
| (1+n)v2 |
| n-2 |
| (1+n)3v |
| n(n-1)(n-2) |
…
同理可得:vn=
| (1+n)n |
| n(n-1)(n-2)…2?1 |
| (1+n)nv |
| n! |
答:
(1)最后面一节车厢脱落后,机车头和剩下的车厢的加速度是
| f |
| nm |
(2)最后面一节车厢脱落后,当它停止运动时,机车头和剩下的车厢的速度是
| 1+n |
| n |
(3)全部车厢脱落并停止运动时,机车头的速度是
| (1+n)nv |
| n! |
点评:本题物理原理比较简单,关键在于运用数学归纳法寻找规律,考查运用数学知识处理物理问题的能力.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目

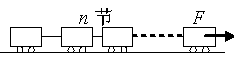
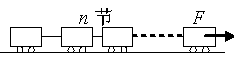 (2)最后面一节车厢脱落后,当它停止运动时,机车头和剩下的车厢的速度是多大?
(2)最后面一节车厢脱落后,当它停止运动时,机车头和剩下的车厢的速度是多大?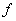 ,行驶中后面有一节车厢脱落,待脱落车厢停止运动时后面又有一节车厢脱落,各节车厢按此方式依次脱落,整个过程中机车头的牵引力保持不变,问:
,行驶中后面有一节车厢脱落,待脱落车厢停止运动时后面又有一节车厢脱落,各节车厢按此方式依次脱落,整个过程中机车头的牵引力保持不变,问: (2)最后面一节车厢脱落后,当它停止运动时,机车头和剩下的车厢的速度是多大?
(2)最后面一节车厢脱落后,当它停止运动时,机车头和剩下的车厢的速度是多大?