题目内容
11.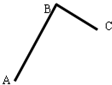 如图,两根长度分别为L1和L2的光滑杆AB和BC在B点垂直焊接,当按图示方式固定在竖直平面内时,将一滑环从B点由静止释放,分别沿BA和BC滑到杆的底端经历的时间相同,则这段时间为( )
如图,两根长度分别为L1和L2的光滑杆AB和BC在B点垂直焊接,当按图示方式固定在竖直平面内时,将一滑环从B点由静止释放,分别沿BA和BC滑到杆的底端经历的时间相同,则这段时间为( )| A. | $\sqrt{\frac{2\sqrt{{L}_{1}{L}_{2}}}{g}}$ | B. | $\sqrt{\frac{\sqrt{2{L}_{1}{L}_{2}}}{g}}$ | ||
| C. | $\sqrt{\frac{2\sqrt{{{L}_{1}}^{2}+{{L}_{2}}^{2}}}{g}}$ | D. | $\sqrt{\frac{2({{L}_{1}}^{2}+{{L}_{2}}^{2})}{g({L}_{1}+{L}_{2})}}$ |
分析 设BA和BC倾角分别为α和β,根据牛顿第二定律求出滑环的加速度,结合时间相等,由位移时间公式对两个过程列式,结合几何关系求解.
解答 解:设BA和BC倾角分别为α和β,根据牛顿第二定律得:
滑环沿BA下滑的加速度为 a1=$\frac{mgsinα}{m}$=gsinα ①
沿BC下滑的加速度为 a2=$\frac{mgsinβ}{m}$=gsinβ ②
设这段时间为t,由题有:
L1=$\frac{1}{2}{a}_{1}{t}^{2}$ ③
L2=$\frac{1}{2}{a}_{2}{t}^{2}$ ④
又据数学知识有:sinα=cosβ ⑤
由③的平方加④的平方,结合⑤解得 t=$\sqrt{\frac{2\sqrt{{{L}_{1}}^{2}+{{L}_{2}}^{2}}}{g}}$
故选:C
点评 本题关键要两个物体的位移关系、加速度关系,由位移时间公式得到时间.要明确物体的位移和加速度都与斜面的倾角有关,所以要用斜面的倾角表示位移和加速度.这种思路和方法要注意积累.

练习册系列答案
相关题目
3.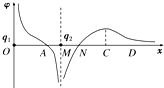 两电荷量分别为q1和q2的点电荷放在x轴上的O、M两点,两电荷连线上各点电势φ随x变化的关系如图所示,其中A、N两点的电势均为零,ND段中的C点电势最高,则( )
两电荷量分别为q1和q2的点电荷放在x轴上的O、M两点,两电荷连线上各点电势φ随x变化的关系如图所示,其中A、N两点的电势均为零,ND段中的C点电势最高,则( )
 两电荷量分别为q1和q2的点电荷放在x轴上的O、M两点,两电荷连线上各点电势φ随x变化的关系如图所示,其中A、N两点的电势均为零,ND段中的C点电势最高,则( )
两电荷量分别为q1和q2的点电荷放在x轴上的O、M两点,两电荷连线上各点电势φ随x变化的关系如图所示,其中A、N两点的电势均为零,ND段中的C点电势最高,则( )| A. | N点的电场强度大小为零 | |
| B. | q1电量小于q2 | |
| C. | NC间场强方向指向x轴负方向 | |
| D. | 将一正点电荷从N点移到D点,电场力先做正功后做负功 |
20.2015年7月15日,美国新视野号(New Horizons)探测号飞掠冥王星,拍下的史上最清晰冥王星照片,人类第一次有机会近距离观察冥王星,已知冥王星的轨道半长轴为59亿千米,目地距离为1.5亿千米,由此可以估算出冥王星的公转周期约为( )
| A. | 50年 | B. | 100年 | C. | 250年 | D. | 500年 |
1.随着世界航空事业的发展,深太空探测已逐渐成为各国关注的热点.假设深太空中有一颗外星球,质量是地球质量的2倍,半径是地球半径的$\frac{1}{2}$.则下述判断正确的有( )
| A. | 该外星球上第一宇宙速度是地球上第一宇宙速度的2倍 | |
| B. | 在地面上所受重力为G的物体,在该外星球表面上所受重力变为2G | |
| C. | 该外星球的同步卫星周期一定小于地球同步卫星周期 | |
| D. | 该外星球上从某高处自由落地时间是地面上同一高处自由落地时间的一半 |
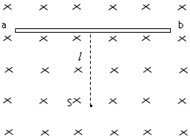 如图,真空室内存在匀强磁场,磁场方向垂直于纸面向里,磁感应强度的大小B=0.60T,磁场内有一块平面感光板ab,板面与磁场方向平行,在距ab的距离l=16cm处,有一个点状的α放射源S,它向各个方向发射α粒子,α粒子的速度都是v=3.0×106m/s,已知α粒子的电荷与质量之比$\frac{q}{m}$=5.0×107C/kg,现只考虑在图纸平面中运动的α粒子,求:
如图,真空室内存在匀强磁场,磁场方向垂直于纸面向里,磁感应强度的大小B=0.60T,磁场内有一块平面感光板ab,板面与磁场方向平行,在距ab的距离l=16cm处,有一个点状的α放射源S,它向各个方向发射α粒子,α粒子的速度都是v=3.0×106m/s,已知α粒子的电荷与质量之比$\frac{q}{m}$=5.0×107C/kg,现只考虑在图纸平面中运动的α粒子,求: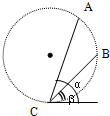 如图所示,A、B、C是同一半径为R的竖直圆周上的三个点,C为最低点,AC、BC为两条分别与水平方向成α、β角的光滑导轨.则物体从A、B点滑到C点所经历的时间之比为1:1,到达C点时的速率之比为$\frac{sinα}{sinβ}$.
如图所示,A、B、C是同一半径为R的竖直圆周上的三个点,C为最低点,AC、BC为两条分别与水平方向成α、β角的光滑导轨.则物体从A、B点滑到C点所经历的时间之比为1:1,到达C点时的速率之比为$\frac{sinα}{sinβ}$. 厦门市BRT(快速公交)于2008年开始运营,其中快1线(第一码头枢纽站-厦门北站)全线共22个站点(包括始发站和终点站).公交车正常运行过程中,进出站时(可视为水平面上的匀变速直线运动)加速度的大小均为2.5m/s2,停站时间40s,其余路段均以45km/h的速率行驶,取g=10m/s2.
厦门市BRT(快速公交)于2008年开始运营,其中快1线(第一码头枢纽站-厦门北站)全线共22个站点(包括始发站和终点站).公交车正常运行过程中,进出站时(可视为水平面上的匀变速直线运动)加速度的大小均为2.5m/s2,停站时间40s,其余路段均以45km/h的速率行驶,取g=10m/s2.