题目内容
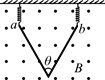
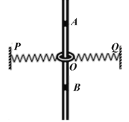
【题目】如图,一个质量为m的刚性圆环套在竖直固定细杆上,圆环的直径略大于细杆的直径,圆环的两边与两个相同的轻质弹簧的一端相连,轻质弹簧的另一端相连在和圆环同一高度的墙壁上的P、Q两点处,弹簧的劲度系数为k,起初圆环处于O点,弹簧处于原长状态且原长为L;将圆环拉至A点由静止释放,OA=OB=L,重力加速度为g,对于圆环从A点运动到B点的过程中,弹簧处于弹性范围内,下列说法正确的是
A.圆环通过O点的加速度小于g
B.圆环在O点的速度最大
C.圆环在A点的加速度大小为g+![]()
D.圆环在B点的速度为2![]()
【答案】D
【解析】
A.圆环通过O点时,水平方向合力为零,竖直方向只受重力,故加速度等于g,故A错误;
B.圆环受力平衡时速度最大,应在O点下方,故B错误;
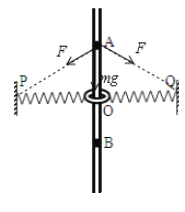
C.圆环在下滑过程中与粗糙细杆之间无压力,不受摩擦力,在A点对圆环进行受力分析如图,根据几何关系,在A点弹簧伸长
![]()
根据牛顿第二定律,有
![]()
解得
![]()
故C错误;
D.圆环从A到B过程,根据功能关系,减少的重力势能转化为动能
![]()
解得
![]()
故D正确。
故选D。

练习册系列答案
相关题目