题目内容
如图所示，宽度为L=0.20m的足够长的平行光滑金属导轨固定在绝缘水平面上，导轨的一端连接阻值为R=1.0Ω的电阻．导轨所在空间存在竖直向下的匀强磁场，磁感应强度大小为B=0.50T．一根质量为m=10g的导体棒ab放在导轨上与导轨接触良好，导轨和导体棒的电阻均可忽略不计．现用一平行于导轨的拉力拉动导体棒沿导轨向右匀速运动，运动速度v=10m/s，在运动过程中保持导体棒与导轨垂直．求：
（1）在闭合回路中产生的感应电流的大小；
（2）作用在导体棒上的拉力的大小；
（3）从某一位置开始记录，当导体棒移动30cm时撤去拉力，直到导体棒静止．求整个过程（从开始记录到棒静止）电阻R上产生的热量．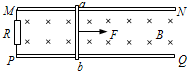
（1）在闭合回路中产生的感应电流的大小；
（2）作用在导体棒上的拉力的大小；
（3）从某一位置开始记录，当导体棒移动30cm时撤去拉力，直到导体棒静止．求整个过程（从开始记录到棒静止）电阻R上产生的热量．
（1）导体棒产生的感应电动势为 E=BLv=1.0V
感应电流为 I
=1.0 A
（2）导体棒匀速运动，安培力与拉力平衡
即有 F=F安=BIL=0.1N
（3）导体棒移动30cm的时间为 t=
=0.03s
根据焦耳定律，Q1=I2R t=0.03J
撤去F后，导体棒做减速运动，其动能转化为内能，则根据能量守恒，有
Q2=
mv2=0.5J
故电阻R上产生的总热量为 Q=Q1+Q2=0.53J
答：
（1）在闭合回路中产生的感应电流的大小为1A；
（2）作用在导体棒上的拉力的大小是0.1N；
（3）整个过程电阻R上产生的热量是0.53J．
感应电流为 I
| E |
| R |
（2）导体棒匀速运动，安培力与拉力平衡
即有 F=F安=BIL=0.1N
（3）导体棒移动30cm的时间为 t=
| l |
| v |
根据焦耳定律，Q1=I2R t=0.03J
撤去F后，导体棒做减速运动，其动能转化为内能，则根据能量守恒，有
Q2=
| 1 |
| 2 |
故电阻R上产生的总热量为 Q=Q1+Q2=0.53J
答：
（1）在闭合回路中产生的感应电流的大小为1A；
（2）作用在导体棒上的拉力的大小是0.1N；
（3）整个过程电阻R上产生的热量是0.53J．
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
如图所示，宽度为L=0.2m的足够长的平行光滑金属导轨固定在绝缘水平面上，导轨的一端连接阻值为R=1.0Ω的电阻．导轨所在空间存在竖直向下的匀强磁场，磁感应强度大小为B=0.2T．一根质量为m=10g的导体棒MN放在导轨上，并与导轨始终接触良好，导轨和导体棒的电阻均可忽略不计．现用垂直MN的水平拉力F拉动导体棒沿导轨向右匀速运动，速度为v=5.0m/s，在运动过程中保持导体棒与导轨垂直．求：
如图所示，宽度为L=0.5m的足够长的平行金属导轨MN、PQ的电阻不计，垂直导轨水平放置一质量为m=0.5kg、电阻为R=4Ω的金属杆CD，导轨上端跨接一个阻值RL=4Ω的灯泡，整个装置处于垂直于导轨平面的匀强磁场中，导轨平面与水平面之间的夹角为θ=60°，金属杆由静止开始下滑，且始终与导轨垂直并良好接触，动摩擦因数为μ=
（2010?济南一模）如图所示，宽度为L=0.20m的足够长的平行光滑金属导轨固定在绝缘水平桌面上，导轨的一端连接阻值为R=0.9Ω的电阻．导轨cd段右侧空间存在垂直桌面向上的匀强磁场，磁感应强度B=0.50T．一根质量为m=10g，电阻r=0.1Ω的导体棒ab垂直放在导轨上并与导轨接触良好．现用一平行于导轨的轻质细线将导体棒ab与一钩码相连，将重物从图示位置由静止释放．当导体棒ab到达cd时，钩码距地面的高度为h=0.3m．已知导体棒ab进入磁场时恰做v=10m/s的匀速直线运动，导轨电阻可忽略不计，取g=10m/s2．求：
如图所示，宽度为L的金属框架竖直固定在绝缘地面上，框架的上端接有一特殊的电子元件，如果将其作用等效成一个电阻，则其阻值与其两端所加的电压成正比，即等效电阻R=kU，式中k为恒量．框架上有一质量为m的金属棒水平放置，金属棒与框架接触良好无摩擦，离地高为h，磁感应强度为B的匀强磁场与框架平面相垂直．将金属棒由静止释放，棒沿框架向下运动．不计金属棒电阻，问：
（2012?盐城三模）如图所示，宽度为L的金属框架竖直固定在绝缘地面上，框架的上端接有一个电子元件，其阻值与其两端所加的电压成正比，即R=kU，式中k为常数．框架上有一质量为m，离地高为h的金属棒，金属棒与框架始终接触良好无摩擦，且保持水平．磁感应强度为B的匀强磁场方向垂直于框架平面向里．将金属棒由静止释放，棒沿框架向下运动，不计金属棒电阻．重力加速度为g．求：