题目内容
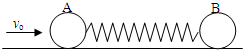 如图所示,光滑的水平面上静置着两个用弹簧连结着的质量均为M的小球A和B,现有一质量为m,速度为v0的子弹水平射入A,并留在其中,求:
如图所示,光滑的水平面上静置着两个用弹簧连结着的质量均为M的小球A和B,现有一质量为m,速度为v0的子弹水平射入A,并留在其中,求:(1)子弹与AB组成的系统动能损失最大时处于什么状态?此时系统动能还有多少?
(2)系统损失的动能有多少转化为内能?
分析:光滑平面上没有摩擦力,子弹射入A后和A组成一个整体,此时只有动能和弹性势能之间的转化;此时整个系统不受其他外力,故总体重量守恒.
解答:解:(1)动能损失最大时,弹簧压缩量最大,对子弹和A有:mv0=(M+m)v1…①
对子弹和A与B的相互作用过程,符合动量守恒,有:(M+m)v1=(2M+m)v2…②
连式①②得:v2=
此时系统还具有动能为:Ek2=
(2M+m)(
)2=
(2)损失的动能转化为内能的过程,只有子弹射入A的过程中发生,其值为:
Q=
mv02-
(M+m)v12=
故答案为:(1)动能损失最大时,弹簧压缩量最大;
.(2)
.
对子弹和A与B的相互作用过程,符合动量守恒,有:(M+m)v1=(2M+m)v2…②
连式①②得:v2=
| mv0 |
| 2M+m |
此时系统还具有动能为:Ek2=
| 1 |
| 2 |
| mv0 |
| 2M+m |
| m2v02 |
| 2(2M+m) |
(2)损失的动能转化为内能的过程,只有子弹射入A的过程中发生,其值为:
Q=
| 1 |
| 2 |
| 1 |
| 2 |
| Mmv02 |
| 2(M+m) |
故答案为:(1)动能损失最大时,弹簧压缩量最大;
| m2v02 |
| 2(2M+m) |
| Mmv02 |
| 2(M+m) |
点评:从动量守恒和能量守恒出发,用整体性和分割法做题即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示.光滑的水平绝缘细杆上套有一圆形的光滑铜环处于静止状态.现在使条形磁铁沿铜环的轴线向左运动,在条形磁铁的N极向左运动至铜环所在竖直平面的过程中,下列说法正确的是( )
如图所示.光滑的水平绝缘细杆上套有一圆形的光滑铜环处于静止状态.现在使条形磁铁沿铜环的轴线向左运动,在条形磁铁的N极向左运动至铜环所在竖直平面的过程中,下列说法正确的是( )| A、铜环中感应电流为图中箭头方向,铜环向右运动 | B、铜环中感应电流与图中箭头方向相反,铜环向左运动 | C、铜环中感应电流与图中箭头方向相反,铜环向右运动 | D、铜环中感应电流为图中箭头方向,铜环向左运动 |

 (2011?河北模拟)如图所示,光滑的水平地面上有一木板,其左端放有一重物,右方有一竖直的墙.重物质量为木板质量的2倍,重物与木板间的动摩擦因数为μ.使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短.求木板从第一次与墙碰撞到再次碰撞所经历的时间.设木板足够长,重物始终在木板上.重力加速度为g.
(2011?河北模拟)如图所示,光滑的水平地面上有一木板,其左端放有一重物,右方有一竖直的墙.重物质量为木板质量的2倍,重物与木板间的动摩擦因数为μ.使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短.求木板从第一次与墙碰撞到再次碰撞所经历的时间.设木板足够长,重物始终在木板上.重力加速度为g.
 (2010?济南模拟)如图所示,光滑的水平地面上有三块材料完全相同的木块A、B、C,质量均为m.中间用细绳l、2连接,现用一水平恒力F作用在C上,三者开始一起做匀加速运动,运动过程中把一块橡皮泥粘在某一木块上面,系统仍加速运动,则下列说法正确的是( )
(2010?济南模拟)如图所示,光滑的水平地面上有三块材料完全相同的木块A、B、C,质量均为m.中间用细绳l、2连接,现用一水平恒力F作用在C上,三者开始一起做匀加速运动,运动过程中把一块橡皮泥粘在某一木块上面,系统仍加速运动,则下列说法正确的是( ) 如图所示,光滑的水平地面上有一较薄的木板,其左端放有一重物,重物可看成质点.右方有一竖直的墙?重物质量为木板质量的2倍,重物与木板间的动摩擦因数为μ,重力加速度为g,使木板与重物以共同的速度v0向右运动,木板长度为
如图所示,光滑的水平地面上有一较薄的木板,其左端放有一重物,重物可看成质点.右方有一竖直的墙?重物质量为木板质量的2倍,重物与木板间的动摩擦因数为μ,重力加速度为g,使木板与重物以共同的速度v0向右运动,木板长度为