��Ŀ����
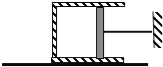
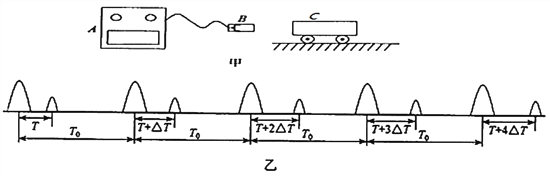
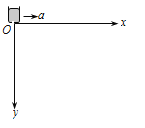
����Ŀ������ͼ��ʾ��ƽ��ֱ������ϵ�ڣ�x��ˮƽ��y����ֱ���¡���ʱ��ʼʱ��λ��ԭ�㴦��ɳ©�ɾ�ֹ�������Լ��ٶ�a��x���ȼ��ٶ��˶����˹�����ɳ��ɳ©��©����ÿ����ȵ�ʱ��©����ͬ������ɳ����֪�������ٶ�Ϊg�����ƿ��������Լ�ɳ���ɳ©�ij��ٶȡ�����˵����ȷ����
A. �������ڵ�ɳ����ȵ�ʱ���ڵ���ֱ��������
B. �������ڵ�ɳ�����ʱ���ڵ�ˮƽ��ౣ�ֲ���
C. t0ʱ��©����ɳ��t��t > t0��ʱ�̵�λ�������� [at0t- ![]() at02��
at02�� ![]() g(t-t0)2]
g(t-t0)2]
D. t0ʱ��©����ɳ��t��t > t0��ʱ�̵�λ�������� [![]() a (t+t0)2��
a (t+t0)2�� ![]() g(t-t0)2]
g(t-t0)2]
���𰸡�AC
������������������������֪��ɳ��©����ˮƽ����������ֱ���˶�����ֱ���������������˶��������˶�ѧ������ʽ����ڣ�t-t0��ʱ����ˮƽ����ֱ�����λ�Ƽ������λ�����꣬�Ӷ�������⣮
©��ɳ������ֱ���������������˶��������ڵĿ��е�ɳ����ȵ�ʱ���ڵ���ֱ�������ӣ�����ˮƽ����������ֱ���˶���������©��ǰˮƽ�������ȼ����˶���������ǵ�ˮƽ������ٶȲ���ȣ��������ʱ���ڵ�ˮƽ����ȣ���A��ȷB�������ȱ���ֱ���˶��Ĺ��ɣ�t0ʱ��©����ɳ����ˮƽ���ٶ�![]() ��ɳ��ɳ©һ���ȼ��ٵ�λ��
��ɳ��ɳ©һ���ȼ��ٵ�λ��![]() ������ɳƽ�ף�tʱ��λ��
������ɳƽ�ף�tʱ��λ��![]() ����
����![]() ��
�� ![]() �����ԣ�
�����ԣ� ![]() ʱ��©����ɳ������Ϊ
ʱ��©����ɳ������Ϊ![]() ����C��ȷD����
����C��ȷD����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�