题目内容
电磁炉专用平底锅锅底和锅壁均由耐高温绝缘材料制成起加热作用的是安在锅底的一系列半径相同的同心导电环导电环所用材料单位长度的电阻为R0=0.125Ω/m,从中心向外第n个同心圆环的半径为rn=(2n-1)r1(n为正整数且n≤7),已知r1=1.0cm.当电磁炉开启后,能产生垂直于锅底方向的变化磁场,已知该磁场的磁感应强度B的变化率为
=100
sinωt(T/s)忽略同心导电圆环感应电流之间的相互影响,
(1)求出半径为rn的导电圆环中产生的感应电动势瞬时值表达式
(2)半径为r1的导电圆环中感应电流的最大值I1m是多大,(取π2=10)
(3)若不计其他损失,所有导电圆环的总电功率P总是多大?
| △B |
| △t |
| 2 |
(1)求出半径为rn的导电圆环中产生的感应电动势瞬时值表达式
(2)半径为r1的导电圆环中感应电流的最大值I1m是多大,(取π2=10)
(3)若不计其他损失,所有导电圆环的总电功率P总是多大?
分析:(1)根据法拉第电磁感应定律,即可求解;
(2)由欧姆定律,结合感应电动势的大小,即可求解;
(3)通过有效值可求出功率,再求出各圈的功率,求出总和.
(2)由欧姆定律,结合感应电动势的大小,即可求解;
(3)通过有效值可求出功率,再求出各圈的功率,求出总和.
解答:解:(1)根据法拉第电磁感应定律,则有:En=
=
=100
πsinωt?π
即其表达式为:100
π2
sinωt(V);
(2)由欧姆定律,则有:I1m=
=
,
解得:I1m=
(3)第n圈电压有效值为:Un=
,
第n圈电阻为:Rn=R0?2πrn,
第n圈功率为:Pn=
,
因此:P总=∑Pn(n=1~7)
答:(1)求出半径为rn的导电圆环中产生的感应电动势瞬时值表达式100
π2
sinωt(V)
(2)半径为r1的导电圆环中感应电流的最大值:I1m=
,
(3)若不计其他损失,所有导电圆环的总电功率P总=∑Pn(n=1~7).
| △? |
| △t |
| △B?Sn |
| △t |
| 2 |
| r | 2 n |
即其表达式为:100
| 2 |
| r | 2 n |
(2)由欧姆定律,则有:I1m=
| E1m |
| R1 |
100
| ||||
| R02πr1 |
解得:I1m=
50
| ||
| R0 |
(3)第n圈电压有效值为:Un=
100
| ||||
|
第n圈电阻为:Rn=R0?2πrn,
第n圈功率为:Pn=
| Un |
| Rn |
因此:P总=∑Pn(n=1~7)
答:(1)求出半径为rn的导电圆环中产生的感应电动势瞬时值表达式100
| 2 |
| r | 2 n |
(2)半径为r1的导电圆环中感应电流的最大值:I1m=
50
| ||
| R0 |
(3)若不计其他损失,所有导电圆环的总电功率P总=∑Pn(n=1~7).
点评:考查法拉第电磁感应定律,闭合电路欧姆定律,掌握有效值与最大值的关系,理解功率与电阻的关系式及求和思想.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
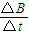 =100
=100 sinωt(T/s)忽略同心导电圆环感应电流之间的相互影响,
sinωt(T/s)忽略同心导电圆环感应电流之间的相互影响, =100
=100 sinωt(T/s)忽略同心导电圆环感应电流之间的相互影响,
sinωt(T/s)忽略同心导电圆环感应电流之间的相互影响,