题目内容
 (2011?江苏)某种加速器的理想模型如图1所示:两块相距很近的平行小极板中间各开有一小孔a、b,两极板间电压uab的变化图象如图2所示,电压的最大值为U0、周期为T0,在两极板外有垂直纸面向里的匀强磁场.若将一质量为m0、电荷量为q的带正电的粒子从板内a孔处静止释放,经电场加速后进入磁场,在磁场中运动时间T0后恰能再次从a 孔进入电场加速.现该粒子的质量增加了
(2011?江苏)某种加速器的理想模型如图1所示:两块相距很近的平行小极板中间各开有一小孔a、b,两极板间电压uab的变化图象如图2所示,电压的最大值为U0、周期为T0,在两极板外有垂直纸面向里的匀强磁场.若将一质量为m0、电荷量为q的带正电的粒子从板内a孔处静止释放,经电场加速后进入磁场,在磁场中运动时间T0后恰能再次从a 孔进入电场加速.现该粒子的质量增加了| 1 | 100 |
(1)若在t=0时刻将该粒子从板内a孔处静止释放,求其第二次加速后从b孔射出时的动能;
(2)现在利用一根长为L的磁屏蔽管(磁屏蔽管置于磁场中时管内无磁场,忽略其对管外磁场的影响),使图1中实线轨迹(圆心为O)上运动的粒子从a孔正下方相距L处的c孔水平射出,请在答题卡图上的相应位置处画出磁屏蔽管;
(3)若将电压uab的频率提高为原来的2倍,该粒子应何时由板内a孔处静止开始加速,才能经多次加速后获得最大动能?最大动能是多少?
分析:(1)求第二次加速后从b孔射出时的动能只需知道加速时所对应的电压,故图2求电压即可.
(2)加入屏蔽管后粒子在屏蔽管中做匀速直线运动,离开屏蔽管后运动轨迹与原来的运动轨迹相似,只是向下平移了l.
(3)从图象可以看出,时间每改变△t=
(图象中为1),电压改变为
U0(图象中为4),
所以图象中电压分别为50,46,42,38,…10,6,2,共13个,
设某时刻t,u=U0时被加速,此时刻可表示为
?N,静止开始加速的时刻t1为t1=
?N-n×
,其中n=12,将n=12代入得t1=
?N-
,因为t1<
,在u>0时,粒子被加速,则最多连续被加速的次数:N=
,
所以只能取N=25,解得t1=
T0,由于电压的周期为
,所以t=
n+
T0(n=0,1,2,3…)
故粒子由静止开始被加速的时刻t=(
+
)T0(n=0,1,2,…)
故加速时的电压分别
U0,
U0,
U0…
U0,
U0,
U0,
加速电压做的总功,即动能的最大值,故粒子的最大动能 Ekm=2×(
+
+…
)qU0+qU0
解得 Ekm=
qU0.
(2)加入屏蔽管后粒子在屏蔽管中做匀速直线运动,离开屏蔽管后运动轨迹与原来的运动轨迹相似,只是向下平移了l.
(3)从图象可以看出,时间每改变△t=
| T0 |
| 100 |
| 2 |
| 25 |
所以图象中电压分别为50,46,42,38,…10,6,2,共13个,
设某时刻t,u=U0时被加速,此时刻可表示为
| T0 |
| 2 |
| T0 |
| 2 |
| 101T0 |
| 100 |
| T0 |
| 2 |
| 1212T0 |
| 100 |
| T0 |
| 2 |
| ||
| △T |
所以只能取N=25,解得t1=
| 19 |
| 25 |
| T0 |
| 2 |
| T0 |
| 2 |
| 19 |
| 25 |
故粒子由静止开始被加速的时刻t=(
| n |
| 2 |
| 19 |
| 50 |
故加速时的电压分别
| 23 |
| 25 |
| 21 |
| 25 |
| 19 |
| 25 |
| 5 |
| 25 |
| 3 |
| 25 |
| 1 |
| 25 |
加速电压做的总功,即动能的最大值,故粒子的最大动能 Ekm=2×(
| 1 |
| 25 |
| 3 |
| 25 |
| 23 |
| 25 |
解得 Ekm=
| 313 |
| 25 |
解答:解:(1)质量为m0的粒子在磁场中作匀速圆周运动Bqv=
,T0=
则T0=
当粒子的质量增加了
m0,其周期增加△T=
T0
根据题图2可知,粒子第一次的加速电压u1=U0
经过
第二次加速,第2次加速电压u2,如图2
在三角形中,
=
=
,
所以粒子第二次的加速电压u2=
U0
粒子射出时的动能 Ek2=qu1+qu2
解得Ek2=
qU0
(2)因为磁屏蔽管使粒子匀速运动至以下L处,出管后仍然做圆周运动,可到C点水平射出.磁屏蔽管的位置如图1所示.粒子运动的轨迹如图3.
(3)如图4(用Excel作图)设T0=100,U0=50,得到在四分之一周期内的电压随时间变化的图象
从图象可以看出,时间每改变△t=
(图象中为1),电压改变为
U0(图象中为4),
所以图象中电压分别为50,46,42,38,…10,6,2,共13个,
设某时刻t,u=U0时被加速,此时刻可表示为
?N,
静止开始加速的时刻t1为t1=
?N-n×
,其中n=12,将n=12代入得t1=
?N-
,
因为t1<
,在u>0时,粒子被加速,则最多连续被加速的次数:N=
,得N=25.
所以只能取N=25,解得t1=
T0,由于电压的周期为
,所以t=
n+
T0(n=0,1,2,3…)
故粒子由静止开始被加速的时刻t=(
+
)T0(n=0,1,2,…)
故加速时的电压分别
U0,
U0,
U0…
U0,
U0,
U0,
加速电压做的总功,即动能的最大值,故粒子的最大动能 Ekm=2×(
+
+…
)qU0+qU0
解得 Ekm=
qU0.

| mv2 |
| r |
| 2πr |
| v |
则T0=
| 2πm0 |
| qB |
当粒子的质量增加了
| 1 |
| 100 |
| 1 |
| 100 |
根据题图2可知,粒子第一次的加速电压u1=U0
经过
| 101T0 |
| 100 |
在三角形中,
| u2 |
| U0 |
| ||||
|
| 24 |
| 25 |

所以粒子第二次的加速电压u2=
| 24 |
| 25 |
粒子射出时的动能 Ek2=qu1+qu2
解得Ek2=
| 49 |
| 25 |
(2)因为磁屏蔽管使粒子匀速运动至以下L处,出管后仍然做圆周运动,可到C点水平射出.磁屏蔽管的位置如图1所示.粒子运动的轨迹如图3.
(3)如图4(用Excel作图)设T0=100,U0=50,得到在四分之一周期内的电压随时间变化的图象
从图象可以看出,时间每改变△t=
| T0 |
| 100 |
| 2 |
| 25 |
所以图象中电压分别为50,46,42,38,…10,6,2,共13个,
设某时刻t,u=U0时被加速,此时刻可表示为
| T0 |
| 2 |
静止开始加速的时刻t1为t1=
| T0 |
| 2 |
| 101T0 |
| 100 |
| T0 |
| 2 |
| 1212T0 |
| 100 |
因为t1<
| T0 |
| 2 |
| ||
| △T |
所以只能取N=25,解得t1=
| 19 |
| 25 |
| T0 |
| 2 |
| T0 |
| 2 |
| 19 |
| 25 |
故粒子由静止开始被加速的时刻t=(
| n |
| 2 |
| 19 |
| 50 |
故加速时的电压分别
| 23 |
| 25 |
| 21 |
| 25 |
| 19 |
| 25 |
| 5 |
| 25 |
| 3 |
| 25 |
| 1 |
| 25 |
加速电压做的总功,即动能的最大值,故粒子的最大动能 Ekm=2×(
| 1 |
| 25 |
| 3 |
| 25 |
| 23 |
| 25 |
解得 Ekm=
| 313 |
| 25 |

点评:本题考查带电粒子在磁场中的圆周运动和在电场中的加速运动以及用数学解决物理问题的能力.关键是判断怎样才能得到最大动能即何时加速,加速电压多大.

练习册系列答案
相关题目
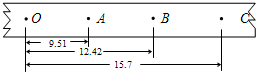 (2011?江苏模拟)在用落体法验证机械能守恒定律时,某同学按照正确的操作选得纸带如图.其中O是起始点,A、B、C是打点计时器连续打下的3个点.该同学用毫米刻度尺测量O到A、B、C各点的距离,并记录在图中(单位cm).
(2011?江苏模拟)在用落体法验证机械能守恒定律时,某同学按照正确的操作选得纸带如图.其中O是起始点,A、B、C是打点计时器连续打下的3个点.该同学用毫米刻度尺测量O到A、B、C各点的距离,并记录在图中(单位cm). (2011?江苏)某同学用如图所示的实验装置验证“力的平行四边形定则”.弹簧测力计A挂于固定点P,下端用细线挂一重物M.弹簧测力计B的一端用细线系于O点,手持另一端向左拉,使结点O静止在某位置.分别读出弹簧测力计A和B的示数,并在贴于竖直木板的白纸上记录O点的位置和拉线的方向.
(2011?江苏)某同学用如图所示的实验装置验证“力的平行四边形定则”.弹簧测力计A挂于固定点P,下端用细线挂一重物M.弹簧测力计B的一端用细线系于O点,手持另一端向左拉,使结点O静止在某位置.分别读出弹簧测力计A和B的示数,并在贴于竖直木板的白纸上记录O点的位置和拉线的方向.
 (2011?江苏模拟)如图所示,小物体放在高度为h=1.25m、长度为S=1.5m的粗糙水平固定桌面的左端A点,以初速度vA=4m/s向右滑行,离开桌子边缘B后,落在水平地面C点,C点与B点的水平距离x=1m,不计空气阻力.试求:(g取10m/s2)
(2011?江苏模拟)如图所示,小物体放在高度为h=1.25m、长度为S=1.5m的粗糙水平固定桌面的左端A点,以初速度vA=4m/s向右滑行,离开桌子边缘B后,落在水平地面C点,C点与B点的水平距离x=1m,不计空气阻力.试求:(g取10m/s2) (2011?江苏)某同学利用如图1所示的实验电路来测量电阻的阻值.
(2011?江苏)某同学利用如图1所示的实验电路来测量电阻的阻值.