Question

【题目】如图所示，水平轨道上有一轻弹簧左端固定，弹簧处于自然状态时，其右端位于P点．现用一质量m=0.1kg的小物块 （可视为质点）将弹簧压缩后释放，物块经过P点时的速度v0=18m/s，经过水平轨道右端Q点后沿半圆轨道的切线进入竖直固定的光滑圆轨道，最后物块经轨道最低点A抛出后落到B点，已知物块与水平轨道间的动摩擦因数μ=0.15，R=l=1m，A到B的竖直高度h=1.25m，取g=10m/s2．

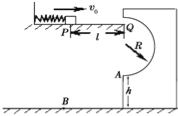
（1）求物块到达Q点时的速度大小（保留根号）；

（2）求物块经过Q点时圆轨道对物块的压力；

（3）求物块水平抛出的位移大小．

Answer 1

【答案】（1）物块到达Q点时的速度大小为m/s；

（2）物块经过Q点时对轨道的压力为31.1N；

（3）物块水平抛出的位移大小为9.5m

【解析】

试题分析：（1）根据动能定理求出物块到达Q点的速度大小；

（2）根据牛顿第二定律求出物块经过Q点时所受的弹力，从而得出物块对Q点的压力；

（3）根据机械能守恒定律求出物块通过最低点A的速度大小，结合平抛运动的规律求出物块水平抛出的位移大小．

解：（1）设物块到达Q点时的速度为v，由动能定理得

﹣μmg l=mv2﹣mv02

代入数据解得v=m/s

（2）设物块刚离开Q点时，圆轨道对物块的压力为FN

根据牛顿定律有FN+mg=m

则FN=m﹣mg=31.1N＞0

故物块能沿圆周轨道运动

（3）设物块到达半圆轨道最低点A时的速度为v1

由机械能守恒得

mv2+mg2R=mv12

解得v1=19 m/s

由 h=gt2

s=vt

得s=v1

代入数据，得s=9.5m．

答：（1）物块到达Q点时的速度大小为m/s；

（2）物块经过Q点时对轨道的压力为31.1N；

（3）物块水平抛出的位移大小为9.5m．