题目内容
电子(不计重力)自静止开始经M、N板间(两板间电压为u)的电场加速后从A点垂直于磁场边界射入宽度为 L的匀强磁场中,电子离开磁场时的位置P偏离入射方向的距离为L,如图所示..(已知电子的质量为m,电量为e)求:
L的匀强磁场中,电子离开磁场时的位置P偏离入射方向的距离为L,如图所示..(已知电子的质量为m,电量为e)求:
(1)电子在加速电场中加速后获得的速度
(2)匀强磁场的磁感应强度
(3)电子在磁场中的运动时间

 L的匀强磁场中,电子离开磁场时的位置P偏离入射方向的距离为L,如图所示..(已知电子的质量为m,电量为e)求:
L的匀强磁场中,电子离开磁场时的位置P偏离入射方向的距离为L,如图所示..(已知电子的质量为m,电量为e)求:(1)电子在加速电场中加速后获得的速度
(2)匀强磁场的磁感应强度
(3)电子在磁场中的运动时间

(1)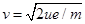 (2)
(2)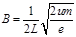 (3)
(3)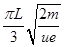
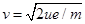 (2)
(2)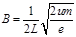 (3)
(3)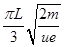
(1)电子在M、N间加速后获得的速度为v,由动能定理得:
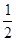 mv2-0="eu " 解得
mv2-0="eu " 解得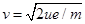 ①
①
(2)电子进入磁场后做匀速圆周运动,设其半径为r,
则:evB=mv2/r②
电子在磁场中的轨迹如图,
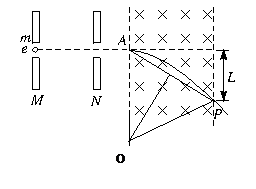
由几何关系得:(r-L)2+ (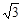 L)2=r2 ③
L)2=r2 ③
由①②③解得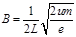
(3) 电子在磁场的周期为T= ,由几何关系得
,由几何关系得 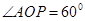
可得电子在磁场中的运动时间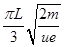
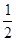 mv2-0="eu " 解得
mv2-0="eu " 解得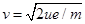 ①
①(2)电子进入磁场后做匀速圆周运动,设其半径为r,
则:evB=mv2/r②
电子在磁场中的轨迹如图,

由几何关系得:(r-L)2+ (
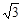 L)2=r2 ③
L)2=r2 ③由①②③解得
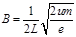
(3) 电子在磁场的周期为T=
 ,由几何关系得
,由几何关系得 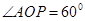
可得电子在磁场中的运动时间
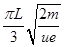

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 射入,从O点沿着与y轴正方向成
射入,从O点沿着与y轴正方向成 夹角射出,求:
夹角射出,求:

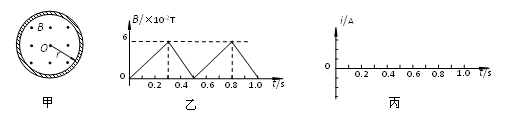
 = 5.0×104 C/kg的带正电粒子,从静止开始经M、N板间的电压U1加速后,沿P、Q板间的中心线进入P、Q间,并最终进入磁场区域.整个装置处于真空中,不计重力影响.
= 5.0×104 C/kg的带正电粒子,从静止开始经M、N板间的电压U1加速后,沿P、Q板间的中心线进入P、Q间,并最终进入磁场区域.整个装置处于真空中,不计重力影响.
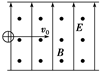

 变化的电压
变化的电压 , 两板间电场可看作是均匀的,且两板外无电场,极板长
, 两板间电场可看作是均匀的,且两板外无电场,极板长 ,板间距离
,板间距离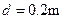 ,在金属板右侧有一边界为
,在金属板右侧有一边界为 的区域足够大的匀强磁场,
的区域足够大的匀强磁场, 垂直,磁感应强度
垂直,磁感应强度 ,方向垂直纸面向里,现有带正电的粒子流沿两板中线
,方向垂直纸面向里,现有带正电的粒子流沿两板中线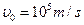 ,比荷
,比荷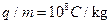 ,重力忽略不计,在每个粒子通过电场区域的极短时间内,电场可视作是恒定不变的.
,重力忽略不计,在每个粒子通过电场区域的极短时间内,电场可视作是恒定不变的.