题目内容
如图所示，一质量为0.5kg的小球，用0.4m长的细线拴住在竖直面内作圆周运动，（1）当小球恰好能通过最高点时的速度为多少？
（2）当小球在最高点速度为4m/s时，细线的拉力是多少？（取g=10m/s2）
分析：（1）当小球恰好过最高点时，绳子的拉力为零，重力提供圆周运动的向心力．根据牛顿第二定律求出最高点的临界速度．
（2）当小球在最高点速度为4m/s时，重力和细线拉力的合力提供向心力，根据牛顿第二定律求出细线的拉力．
（2）当小球在最高点速度为4m/s时，重力和细线拉力的合力提供向心力，根据牛顿第二定律求出细线的拉力．
解答：解：（1）当细线拉力为零时，有：mg=m
解得v0=
=2m/s．
故小球恰好能通过最高点时的速度为2m/s．
（2）根据牛顿第二定律得，mg+T=m
解得T=15N．
故细线的拉力是15N．
| v02 |
| r |
解得v0=
| gr |
故小球恰好能通过最高点时的速度为2m/s．
（2）根据牛顿第二定律得，mg+T=m
| v2 |
| r |
解得T=15N．
故细线的拉力是15N．
点评：解决本题的关键知道小球在竖直面内做圆周运动，靠沿半径方向的合力提供向心力．
练习册系列答案
相关题目
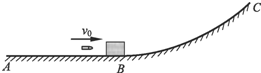如图所示，一质量为0.99kg的木块静止在水平轨道AB的B端，水平轨道与半径为10m的光滑弧形轨道BC相切．现有一质量为10g的子弹以500m/s的水平速度从左边射入木块且未穿出．已知木块与水平轨道的动摩擦因数μ=0.5，g=10m/s2．求：
如图所示，一质量为0.5kg的小球，用0.4m长的细线拴住在竖直面内作圆周运动，g取10m/s2求：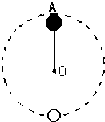
如图所示，一质量为0.5kg的小球，用0.4m长的细线拴住在竖直面内作圆周运动，小球在圆上最高点速度为4m/s．求：（g=10m/s2）