题目内容
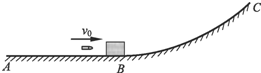 如图所示,一质量为0.99kg的木块静止在水平轨道AB的B端,水平轨道与半径为10m的光滑弧形轨道BC相切.现有一质量为10g的子弹以500m/s的水平速度从左边射入木块且未穿出.已知木块与水平轨道的动摩擦因数μ=0.5,g=10m/s2.求:
如图所示,一质量为0.99kg的木块静止在水平轨道AB的B端,水平轨道与半径为10m的光滑弧形轨道BC相切.现有一质量为10g的子弹以500m/s的水平速度从左边射入木块且未穿出.已知木块与水平轨道的动摩擦因数μ=0.5,g=10m/s2.求:(1)子弹射入木块与木块获得的共同速率;
(2)子弹射入后与木块在圆弧轨道上升的最大高度;
(3)从木块返回B点到静止在水平面上,摩擦阻力的冲量的大小.
分析:(1)子弹射入木块的过程,系统动量守恒,由动量守恒定律求子弹射入木块与木块获得的共同速率;
(2)子弹与木块在光滑弧形轨道BC上运动,到达最高点的过程中,轨道BC的支持力不做功,只有重力做功,系统机械能守恒,即可由机械能守恒列式求出最大高度.
(3)木块返回B点到静止在水平面上,由牛顿第二定律和运动学公式求运动时间,再由I=μ(M+m)gt求摩擦阻力的冲量.
(2)子弹与木块在光滑弧形轨道BC上运动,到达最高点的过程中,轨道BC的支持力不做功,只有重力做功,系统机械能守恒,即可由机械能守恒列式求出最大高度.
(3)木块返回B点到静止在水平面上,由牛顿第二定律和运动学公式求运动时间,再由I=μ(M+m)gt求摩擦阻力的冲量.
解答:解:(1)设子弹射入木块与木块获得的共同速度为v,子弹射入木块前后系统动量守恒,则有
mv0=(m+M)v
解得,v=5m/s
(2)设木块上升最大高度为h,子弹与木块在光滑弧形轨道BC上运动,到达最高点的过程中系统机械能守恒,则有
(M+m)v2=(M+m)gh
解得,h=1.25m
(3)木块返回B点进入水平轨道上作匀减速运动最终静止,设摩擦力的冲量为I,由牛顿第二定律、匀变速运动规律得
a=
=5m/s2
t=
=1s
则摩擦阻力的冲量大小 I=μ(M+m)gt
解得I=5N?S
答:
(1)子弹射入木块与木块获得的共同速率是5m/s;
(2)子弹射入后与木块在圆弧轨道上升的最大高度是1.25m;
(3)从木块返回B点到静止在水平面上,摩擦阻力的冲量的大小是5N?S.
mv0=(m+M)v
解得,v=5m/s
(2)设木块上升最大高度为h,子弹与木块在光滑弧形轨道BC上运动,到达最高点的过程中系统机械能守恒,则有
| 1 |
| 2 |
解得,h=1.25m
(3)木块返回B点进入水平轨道上作匀减速运动最终静止,设摩擦力的冲量为I,由牛顿第二定律、匀变速运动规律得
a=
| f |
| M+m |
t=
| v |
| a |
则摩擦阻力的冲量大小 I=μ(M+m)gt
解得I=5N?S
答:
(1)子弹射入木块与木块获得的共同速率是5m/s;
(2)子弹射入后与木块在圆弧轨道上升的最大高度是1.25m;
(3)从木块返回B点到静止在水平面上,摩擦阻力的冲量的大小是5N?S.
点评:本题首先要正确分析物体的运动过程,其次要准确把握每个过程所遵守的物理规律.对于子弹打出木块过程,往往动量守恒.

练习册系列答案
相关题目
 如图所示,一质量为0.5kg的小球,用0.4m长的细线拴住在竖直面内作圆周运动,
如图所示,一质量为0.5kg的小球,用0.4m长的细线拴住在竖直面内作圆周运动, 如图所示,一质量为0.5kg的小球,用0.4m长的细线拴住在竖直面内作圆周运动,g取10m/s2求:
如图所示,一质量为0.5kg的小球,用0.4m长的细线拴住在竖直面内作圆周运动,g取10m/s2求: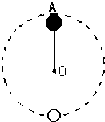 如图所示,一质量为0.5kg的小球,用0.4m长的细线拴住在竖直面内作圆周运动,小球在圆上最高点速度为4m/s.求:(g=10m/s2)
如图所示,一质量为0.5kg的小球,用0.4m长的细线拴住在竖直面内作圆周运动,小球在圆上最高点速度为4m/s.求:(g=10m/s2)