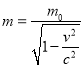��Ŀ����
����Ŀ�������˶���һ��մ̼����˶��������������ϲ������ͼ�ǻ����˶��Ĺ����AB��CD��һ��Բ���ι����BC��һ�γ�7m��ˮƽ�����һ�˶�Ա��AB�����P����6m/s���ٶ��»�����BC��������CD�������Q��ʱ�ٶȼ�Ϊ�㣮��֪�˶�Ա������50kg��h=1.4m��H=1.8m������Բ������ϵ�Ħ������g=10m/s2����
��1���˶�Ա��һ�ξ���B�㡢C��ʱ���ٶȸ��Ƕ��٣�
��2���˶�Ա��BC����Ķ�Ħ��������
��3���˶�Ա���ͣ��BC����Ͼ�BΪ�����״���
���𰸡�
��1���⣺��ˮƽ���Ϊ�������棬�˶�Ա��A��B�Ĺ��̣����ݻ�е���غ㶨�ɣ��У�
![]() mvP2+mgh=
mvP2+mgh= ![]() mvB2
mvB2
�������ݽ�ã�vB=8 m/s
��C��Q�Ĺ����У��У�
![]() mvC2=mgH
mvC2=mgH
�������ݽ�ã�vC=6 m/s��
���˶�Ա��һ�ξ���B�㡢C��ʱ���ٶȸ���8 m/s��6 m/s��
��2����B��C�����У��ɶ��ܶ����У�
����mgs= ![]() mvC2��
mvC2�� ![]() mvB2
mvB2
�������ݽ�ã���=0.2��
���˶�Ա��BC����Ķ�Ħ��������0.2��
��3�����˶�Ա��BC���е���·��Ϊs����
���������̣��������غ�֪����е�ܵļ�����������Ħ�������������ܣ����У�
��mgs��= ![]() mvP2+mgh
mvP2+mgh
�������ݽ�ã�s��=16 m
n= ![]() =2
=2 ![]()
���˶�Ա���ͣ�ھ�B��2 m�ĵط���
���˶�Ա���ͣ��BC����Ͼ�BΪ2 m��
����������1��һ�˶�Ա��AB�����P���»����˶������л�е���غ㣬ȡˮƽ���Ϊ�������棬�������B��ʱ���ٶȣ���C��Q�Ĺ����У�����ȫ��ת��Ϊ�������ܣ��������C����ٶȡ�
��2����B��C�����У����ݶ��ܶ�����ʽ����ֱ������˶�Ա��BC����Ķ�Ħ��������
��3���˶�Ա��BC���е��������������غ㣬��е�ܵļ�����������Ħ�������������ܣ���ʽ�ӿ�������˶�Ա��BC���е���·�̣��ٳ���һ�ε�·�̼�����⡣

 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�