题目内容
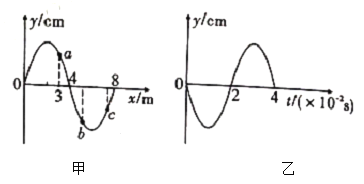
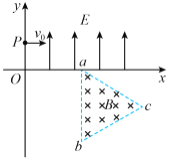
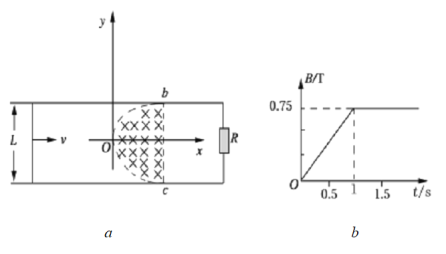
【题目】如图（a）所示，平行长直金属导轨水平放置，间距L=0.4m，导轨右端接有阻值R=1Ω的电阻，导体棒垂直放置在导轨上，且接触良好，导体棒及导轨的电阻均不计，导轨间有边界为抛物线形bOc方向竖直向下的匀强磁场区域，O为抛物线顶点，抛物线方程为x=10y2，磁场区域面积为
。bc两点在导轨上且连线与导轨垂直，长度也为L，从t=0时刻开始，磁感应强度B的大小随时间t变化，规律如图（b）所示；t=0时刻，棒从导轨左端开始以v=1m/s向右匀速运动。t=1s时棒刚好进入磁场，立刻给棒施加一水平向右随x变化的外力F（x）使棒在磁场中沿导轨始终以速度v=1m/s做直线运动，（提示：可以用F－x图象下的“面积”代表力F做的功）求：
(1)棒进入磁场前，回路中的感应电动势E；
(2)棒在运动过程中受到安培力F的最大值；
(3)F（x）的表达式；
(4)棒开始运动后的1.4s内，电阻R产生的焦耳热Q。
【答案】(1)0.08V(2)0.09N(3)
(4)
【解析】
(1)棒进入磁场前
代入数据得电动势大小
(2)根据题意可知，棒在bc位置时，安培力最大，因为此时的感应电动势为
E=BLv
根据欧姆定律有
安培力大小为
联立得
(3)导体棒在磁场中匀速运动
因为
联立解得：
(4)0－1s内的焦耳热
1s到1.4s内外力F(x)做功等于生成的焦耳热
，该段时间棒匀速运动的位移为
则
所以电阻R产生的焦耳热
名师导航单元期末冲刺100分系列答案
【题目】某同学利用如图所示的向心力演示器定量探究匀速圆周运动所需向心力F跟小球质量m、转速n和运动半径r之间的关系。
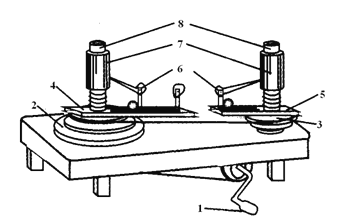
(1)为了单独探究向心力跟小球质量的关系，必须用________法；
(2)转动手柄可以使长槽和短槽分别随变速塔轮匀速转动，槽内的球随之做匀速圆周运动。这时我们可以看到弹簧测力筒上露出标尺，通过标尺上红白相间等分格数，即可求得两个球所受的________；
(3)该同学通过实验得到如下表的数据：
次数 | 球的质量m/g | 转动半径r/cm | 转速/每秒几圈 | 向心力大小F/红格数 |
1 | 14.0 | 15.00 | 1 | 2 |
2 | 28.0 | 15.00 | 1 | 4 |
3 | 14.0 | 15.00 | 2 | 8 |
4 | 14.0 | 30.00 | 1 | 4 |
根据以上数据，可归纳概括出向心力F跟小球质量m、转速n和运动半径r之间的关系是： ___________________（文字表述）；
(4)实验中遇到的问题有：_________（写出一点即可）。
