题目内容
6. 如图所示,轻绳的A端固定在天花板上,B端系一个重力为G的小球,小球静止在固定的光滑的大球球面上,已知AB绳长为l,大球半径为R,天花板到大球顶点的竖直距离AC=d,∠ABO=90°,求绳对小球的拉力和大球对小球的支持力的大小(小球可视为质点)
如图所示,轻绳的A端固定在天花板上,B端系一个重力为G的小球,小球静止在固定的光滑的大球球面上,已知AB绳长为l,大球半径为R,天花板到大球顶点的竖直距离AC=d,∠ABO=90°,求绳对小球的拉力和大球对小球的支持力的大小(小球可视为质点)
分析 分析小球的受力情况,作出力图,根据平衡条件,运用三角形相似法求解绳中张力T和大球对小球的支持力N.
解答  解:分析小球的受力情况:重力G,绳中张力T和大球对小球的支持力N,作出力图,如图.
解:分析小球的受力情况:重力G,绳中张力T和大球对小球的支持力N,作出力图,如图.
根据平衡条件得知,T与N的合力与重力大小相等,方向相反,即有F=G.根据△FNB∽△ABO得
$\frac{N}{OB}=\frac{T}{AB}=\frac{F}{AO}$
又OB=R,AB=L,AO=R+d,F=G,
代入解得:T=$\frac{LG}{R+d}$,N=$\frac{RG}{R+d}$
答:绳对小球的拉力大小为$\frac{LG}{R+d}$,大球对小球的支持力的大小为$\frac{RG}{R+d}$.
点评 本题中T与N不垂直,采用三角形相似法列方程,是常用的方法,考查运用数学知识解决物理问题的能力.

练习册系列答案
相关题目
17.关于平抛运动,下列说法中正确的是( )
| A. | 平抛运动是匀速运动 | |
| B. | 平抛运动是匀变速曲线运动 | |
| C. | 平抛运动不是匀变速运动 | |
| D. | 做平抛运动的物体落地时速度方向可能是竖直向下的 |
14.轻质弹性绳呈水平状,绳的中点为M,两端P、Q同时开始上下振动,一段时间后产生的波形如图,以下判断正确的是( )


| A. | 波源P的起振方向竖直向上 | B. | 波源Q产生的波先到达中点M | ||
| C. | 波传至M点后,M点的振动始终加强 | D. | 波源P的频率是波源Q的频率的两倍 |
1. 将一小球从高处水平抛出,最初2s内小球动能Ek随时间t变化的图线如图所示,不计空气阻力,重力加速度g=10m/s2.根据图象信息,不能确定的物理量是( )
将一小球从高处水平抛出,最初2s内小球动能Ek随时间t变化的图线如图所示,不计空气阻力,重力加速度g=10m/s2.根据图象信息,不能确定的物理量是( )
 将一小球从高处水平抛出,最初2s内小球动能Ek随时间t变化的图线如图所示,不计空气阻力,重力加速度g=10m/s2.根据图象信息,不能确定的物理量是( )
将一小球从高处水平抛出,最初2s内小球动能Ek随时间t变化的图线如图所示,不计空气阻力,重力加速度g=10m/s2.根据图象信息,不能确定的物理量是( )| A. | 小球的质量 | |
| B. | 小球的初速度 | |
| C. | 小球抛出时的高度 | |
| D. | 最初2 s内重力对小球做功的平均功率 |
18.两小球a,b在光滑的水平面上相向运动,碰撞后a球变为静止,b球仍然运动,则碰撞前( )
| A. | a球的动量大于b球的动量 | B. | b球的动量大于a球的动量 | ||
| C. | a球的速度大于b球的速度 | D. | b球的速度大于a球的速度 |
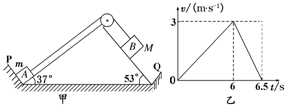 如图甲所示,固定在地面上的三角形斜面体,左斜面光滑,右斜面粗糙,倾角如图.物体A放在左斜面底端挡板P处,通过不可伸长的轻质细绳跨过光滑轻质滑轮与物体B相连接,绳绷直时B离斜面底端挡板Q有一段距离.在t=0时刻,无初速度释放B,根据固定在A上的速度传感器得到的数据,绘出物体A在6.5s内沿斜面运动的速度随时间的v-t图象如图乙所示.已知:每次B碰撞挡板Q后均不粘连、不反弹;每次绳子突然绷紧时,A、B的速度大小立即变为绷紧前瞬间A物体速度大小的一半;A的质量m=2kg,B的质量M=2kg,g=10m/s2,sin 37°=0.6,cos 37°=0.8.求:
如图甲所示,固定在地面上的三角形斜面体,左斜面光滑,右斜面粗糙,倾角如图.物体A放在左斜面底端挡板P处,通过不可伸长的轻质细绳跨过光滑轻质滑轮与物体B相连接,绳绷直时B离斜面底端挡板Q有一段距离.在t=0时刻,无初速度释放B,根据固定在A上的速度传感器得到的数据,绘出物体A在6.5s内沿斜面运动的速度随时间的v-t图象如图乙所示.已知:每次B碰撞挡板Q后均不粘连、不反弹;每次绳子突然绷紧时,A、B的速度大小立即变为绷紧前瞬间A物体速度大小的一半;A的质量m=2kg,B的质量M=2kg,g=10m/s2,sin 37°=0.6,cos 37°=0.8.求: 如图所示,小物体A与水平转盘间的最大静摩擦力Ff=5N,A与转盘圆心间的距离为0.5m,A的质量为m=1kg,且和一端固定在圆心的弹簧相连,弹簧的自然长度为l0=0.4m,劲度系数为k=100N/m,如果转盘转动时,小物体A随转盘转动且不打滑,则转盘转动角速度的范围是多少?
如图所示,小物体A与水平转盘间的最大静摩擦力Ff=5N,A与转盘圆心间的距离为0.5m,A的质量为m=1kg,且和一端固定在圆心的弹簧相连,弹簧的自然长度为l0=0.4m,劲度系数为k=100N/m,如果转盘转动时,小物体A随转盘转动且不打滑,则转盘转动角速度的范围是多少?